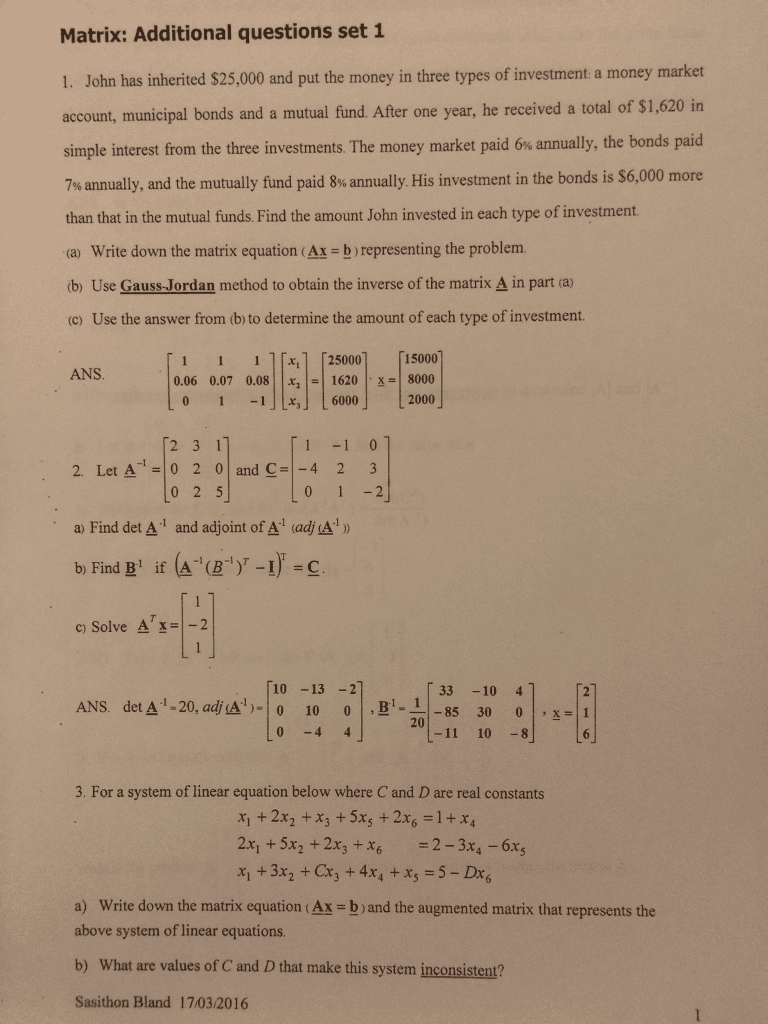MAT223H1 Lecture Notes - Main Diagonal, Mexican Peso, Algebraic Structure
Document Summary
A solution is a vector (t1,t2,,tn) rn that satisfies all the equations. If the set of solutions is s = then we say that the system is inconsistent. Note that the above system can be represented as follows: a11 a12 a1n | b1 a21 a22 a2n | b2 am1 am2 amn | bm. Two systems of linear equations are said to be equivalent if and only if they have the same set of solutions. Main diagonal of c is (1 8 4) If a mmxn and m = n then we say that a is a square matrix of order n. Let a mnxn: a is said to be diagonal if and only if all the elements out of the main diagonal are zero. The main diagonal can have zeroes: a is said to be upper triangular if and only id all its entries below the main diagonal are zero.
