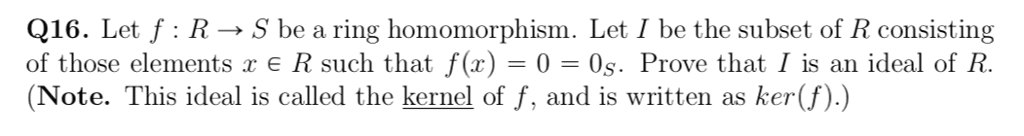MA100 Lecture Notes - Subset, Natural Number, Empty Set
Document Summary
A set is a collection of objects called the elements or members of the set. A= {alice, bob, cameron} - order doesn"t matter. Sets can be written using a property b= {integers x such that 2 x 6} 10 \b 10 is not in the set. A set that has no elements is called the empty set or the void set and is denoted . Two sets are equal if they have exactly the same elements. If c= {6, 3, 4, 5, 2} then c=b. If d= {2, 3, 4, 5, 7} then d b. If e= {2, 3, 4, 5} then e b. However e is a subset of b, we write e _ b (a set is a subset of itself) _ b. Since e b we can write e b and we can say that e is a proper subset of b.