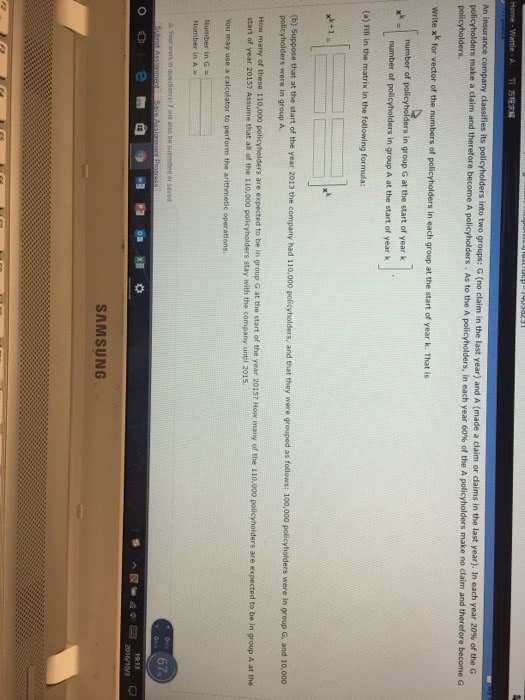
ADMS 3530 Lecture Notes - Money Market Fund, Risk Premium, Chc Helicopter
Document Summary
The risks of deaths of individual policyholders are largely independent, and therefore are diversifiable. Therefore, the insurance company is satisfied to charge a premium that reflects actuarial probabilities of death, without an additional risk premium. In contrast, flood damage is not independent across policyholders. If my coastal home floods in a storm, there is a greater chance that my neighbor"s will too. Because flood risk is not diversifiable, the insurance company may not be satisfied to charge a premium that reflects only the expected value of payouts. The actual returns on the snake oil fund exhibit considerable variation around the regression line. This indicates that the fund is subject to diversifiable risk: it is not well diversified. The variation in the fund"s returns is influenced by more than just market-wide events. Investors would buy shares of firms with high degrees of diversifiable risk, and earn high- risk premiums.