CHEM 11b Lecture 9: Chem13
9 Mar 2017
School
Department
Course
Professor
Document Summary
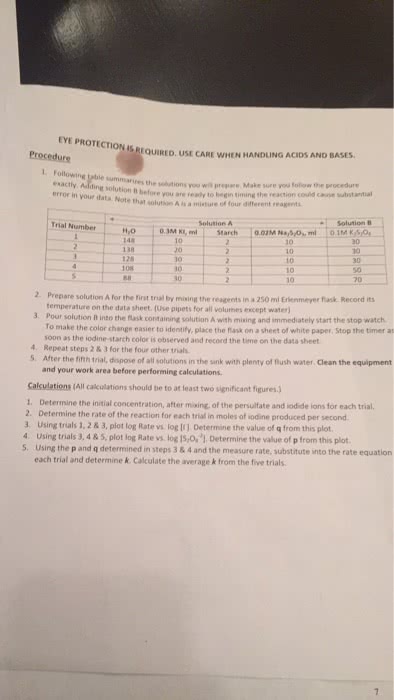
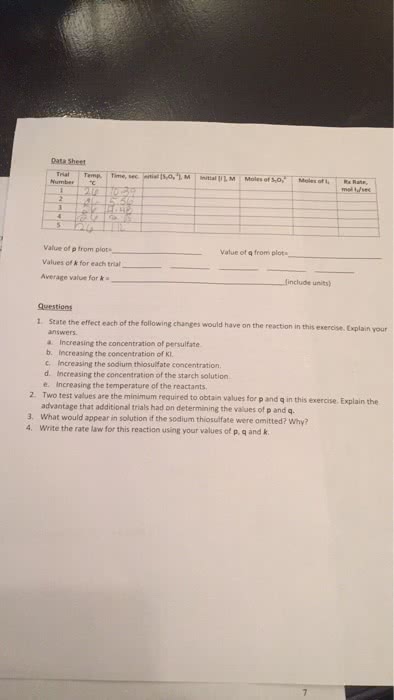
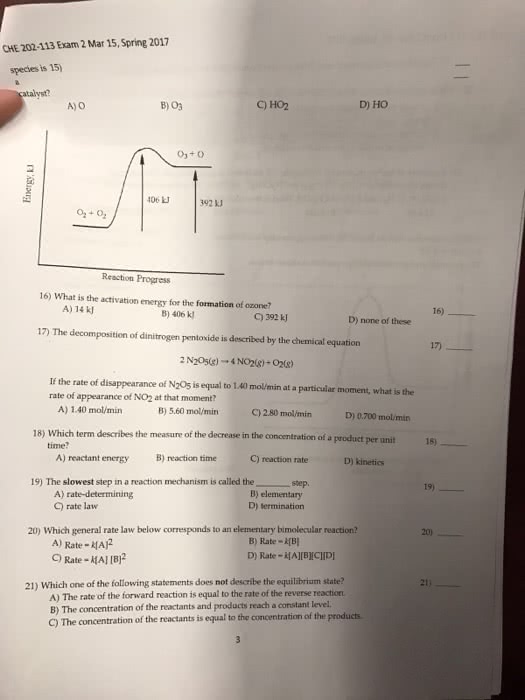
In chemical kinetics we study rates of chemical reactions. Rate is the change in a measurable property per unit time. Absorbance per minute could track the color changes. Atmospheres per second could track a gas-evolving reaction. Changes in concentration of a species over time (m/s) Rate = - change in / change in time. Negative sign indicates the disappearance of a reactant which allows it to be expressed as a positive value. If it is the rate of a product and is increasing then don"t put a negative. The two rates are not the same. General rate expression for a reaction, divide the rate of disappearance of each reactant and appearance of each product by its stoichiometric coefficient. Overall rate expression uses coefficients to make it clearer. General rate expression!! aa + bb + cc + dd. Multiply each rate by the inverse of its stoichiometric coefficient. Put a negative sign to indicate the disappearance of a reactant.
