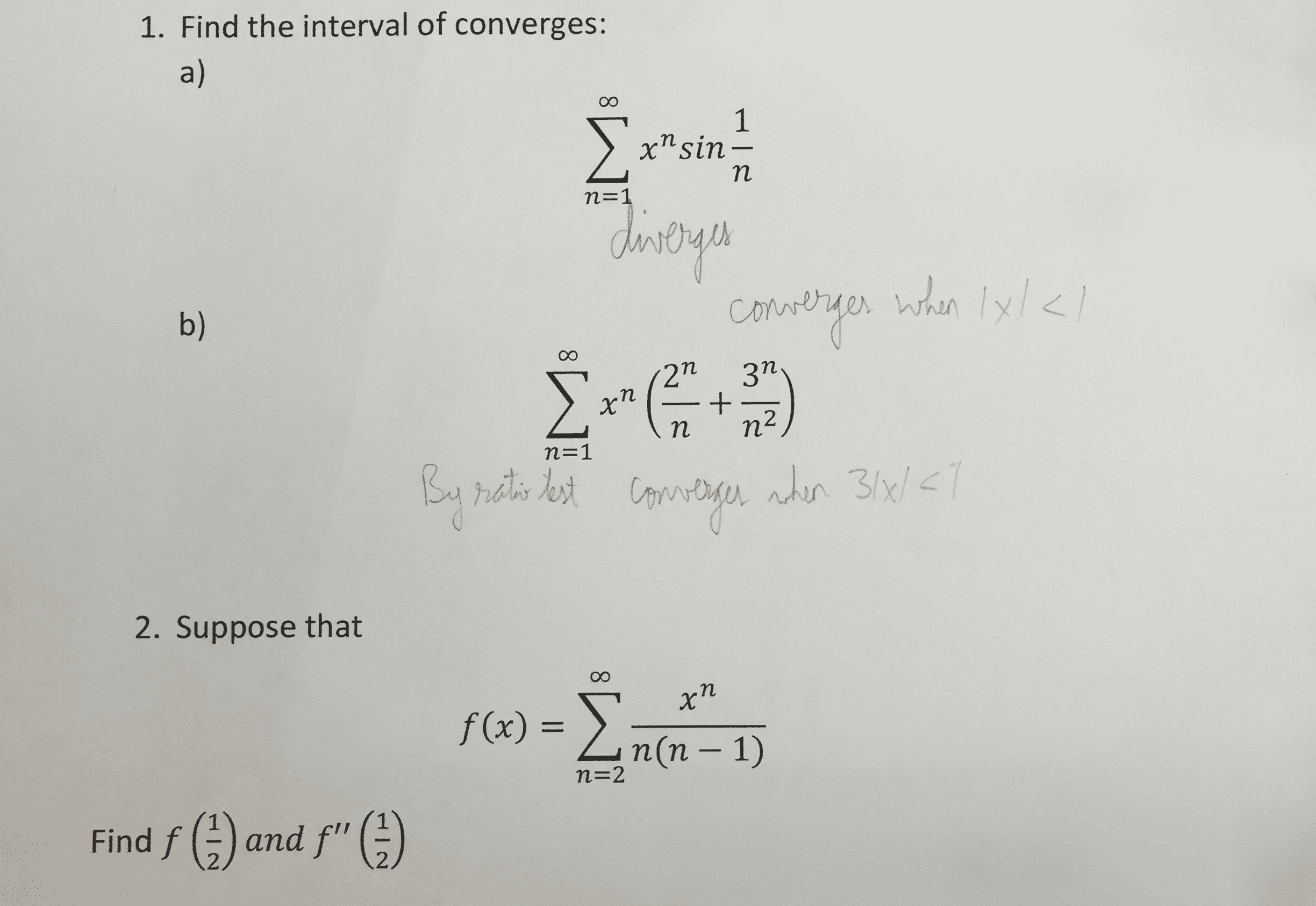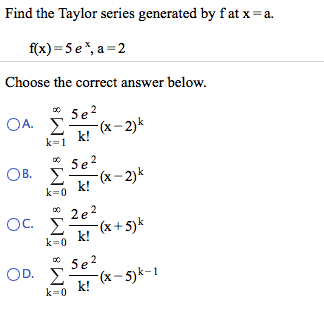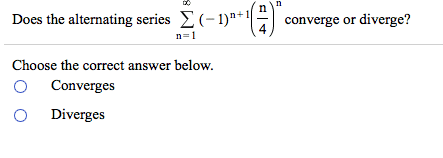here is the problem it is already solved and this is the yahooanswer solution and my teachers solution as well. All i need is aGraph and for someone to explain how my teachergot 0,0 and 0,-2 as intresection points.

teachers solution:find all 4 points of intersections: (0,0),(0,-2), (-4sqrt(17sqrt(2)-24), 10sqrt(2)-14),(-4sqrt(17sqrt(2)-24), 10sqrt(2)-14).
yahoo answers:sin(theta) = r^2/4 ==> sin(theta)>= 0 . Hence 0 =< theta =< pi
r = 1 - sin(theta) ; therefore 0 =< r =< 1, because now weknow 0 =< sin(theta) =< 1
Therefore y = r sin(theta) >= 0 so the intersection points are in theupper half plane.
Also, sin(theta) = r^2/4 =< 1/4 < 1/sqrt(2) = sin pi/4 =sin(3pi/4),
so 0 =< theta < pi/4 or 3pi/4 < theta =< pi.
---
At an intersection point, sin(theta) = r^2/4 = 1 - r
r^2 + 4r - 4 = 0
Roots: r = -- 2 +/- 2 sqrt(2); but r >= 0, so r = 2 sqrt(2) - 2= 2(sqrt(2) - 1)
sin(theta) = 1 - r = 3 - 2 sqrt(2)
There is just one value of y, namely
y = r sin(theta) = 2 (sqrt(2) - 1)(3 - 2 sqrt(2) ) = 2 (5 sqrt(2) -7) = 10 sqrt(2) - 14
( or y = 10 (sqrt(2) - 1.4 ) = 0.142135...
However, there are two intersection points, with x^2 = r^2 -y^2
x = +/- sqrt( r^2 - y^2 )
x^2 = r^2 - y^2 = 4 (sin theta) -- y^2 = 4 (3 - 2 sqrt(2)) -- [2(5sqrt(2) - 7)]^2
x^2 = 12 - 8 sqrt(2) -4 [ 99 - 70 sqrt(2)] = 272 sqrt(2) - 384 (=17 x 2^4 sqrt(2) - 3 x 2^7)
x = +/- 4 sqrt(17 sqrt(2) - 24) [ = +/- 0.8161427...]