ZOL 355 Lecture Notes - Lecture 17: Logistic Function, Exponential Growth, Loggerhead Sea Turtle

Lecture 17: Population Ecology, Logistic Growth
• Brief Review: Exponential & Geometric Growth Equations for Estimating
Population Size N and Growth Rate r or λ
• Assumptions of the exponential growth equation
o When is the exponential growth equation a reasonable model for
population growth?
o All populations have the potential for exponential growth but
o this is not the case for long, Why?
▪ There is a limit to the population; space, food, etc.
find more resources at oneclass.com
find more resources at oneclass.com
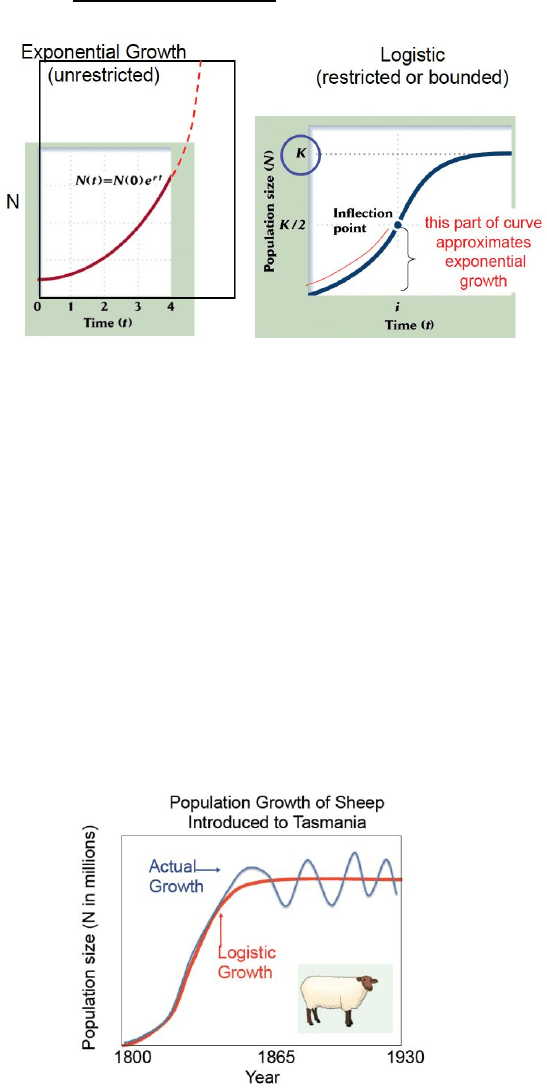
• Population growth is limited by the carrying capacity or K such populations
experience logistic growth.
o Comparison of logistic and exponential growth curves
▪ Carrying Capacity - the maximum amount a population can be
▪ K is a population size that has reached its max size
o Comparison of equations for population growth rate for logistic and
exponential growth
▪ Exponential Growth Logistic
▪ (unrestricted) (restricted or bounded)
▪ dN/dt = rN dN/dt = rN(1 – N/K)
▪ K = carrying capacity
▪ What happens to N and dN/dt if N=K?
• Population is not growing - its zero
▪ What happens to N and dN/dt if N<K?
• Population is decreasing
▪ What happens to N and dN/dt if N>K?
• Population is increasing
o K is the carrying capacity but also the equilibrium population size
find more resources at oneclass.com
find more resources at oneclass.com



