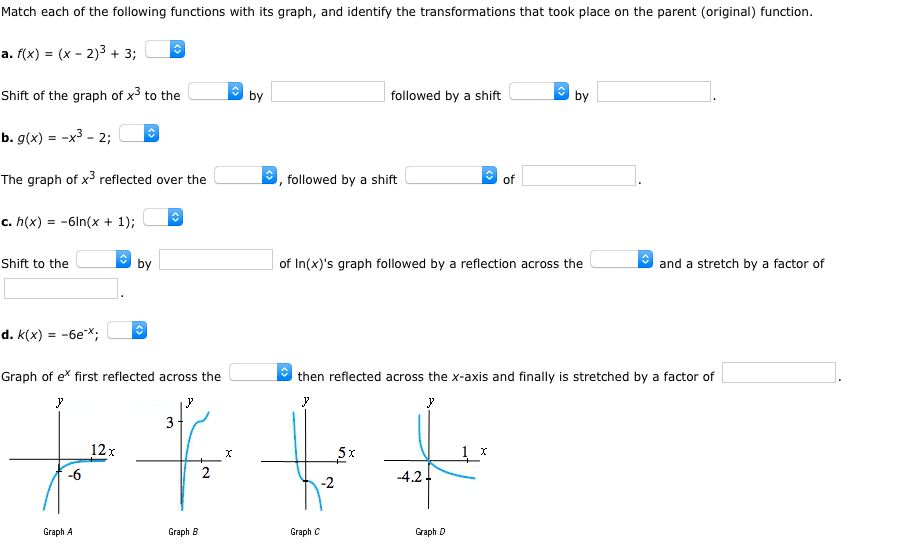
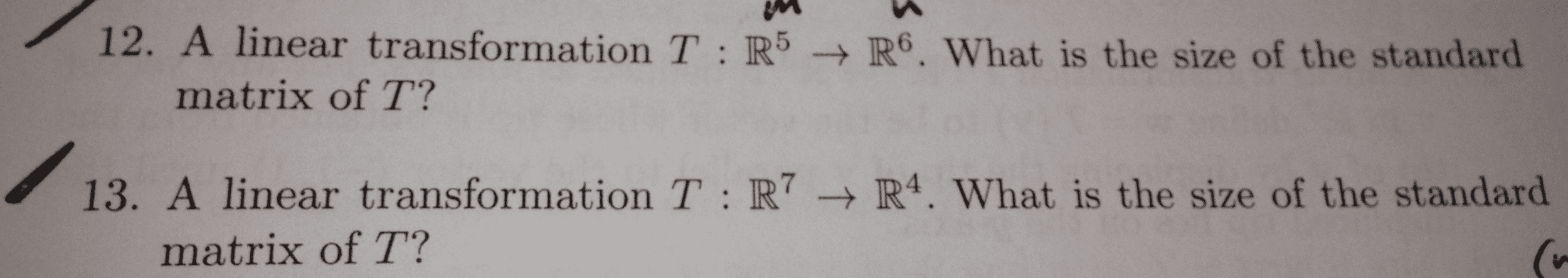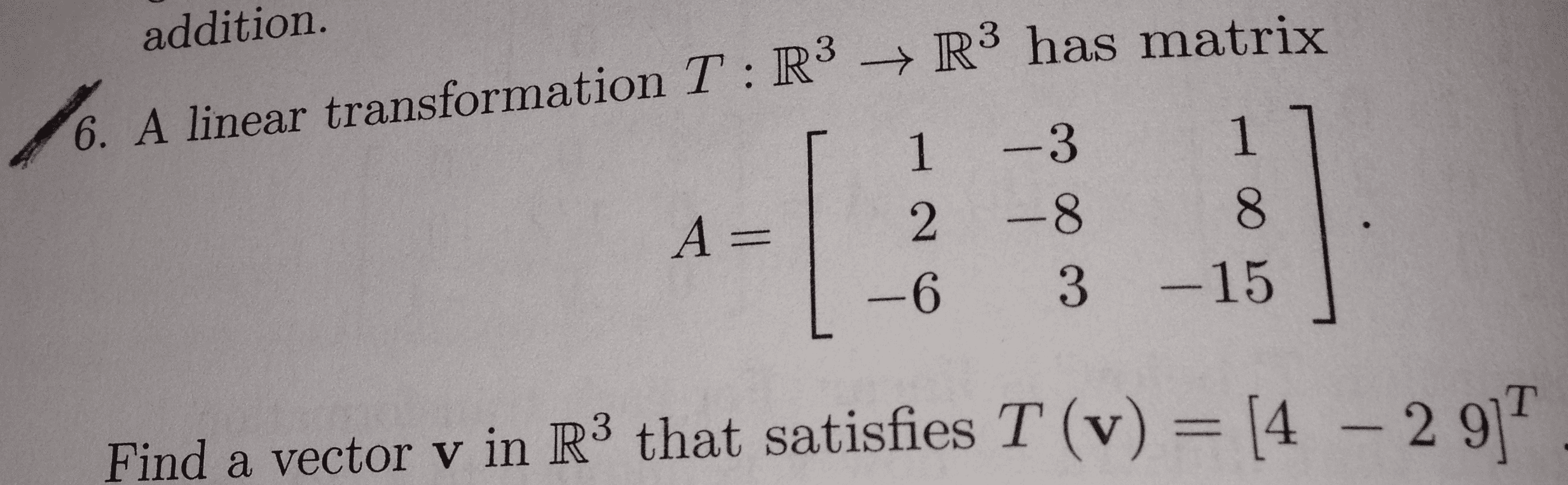MA 108 Lecture 1: Compositions of Transformations- Emily
31 Jan 2019
School
Department
Course
Professor
Document Summary
An important type of composition is a glide reflection, which is a translation followed by: compositions: when two or more transformations are combined to produce a single transformation, the result is called a composition of the transformations. The composition of two or more isometries is also an isometry. Compositions may preserve or reverse orientation depending on how many reflections they contain. a reflection in a line parallel to the direction of the translation. A glide reflection is an isometry that reverses the orientation of figures. For example, suppose a translation 6 units to the right is followed by a reflection in the x-axis. This glide reflection can be written in coordinate form as (x",y") = ( x + 6, -y ). The glide reflection ( x", y" ) = ( -x, y +4 ) is a translation 4 units up followed by a reflection in the y-axis.
