MATH 2B Lecture Notes - Lecture 2: Farad, Riemann Sum
MATH 2B verified notes
2/30View all
Document Summary
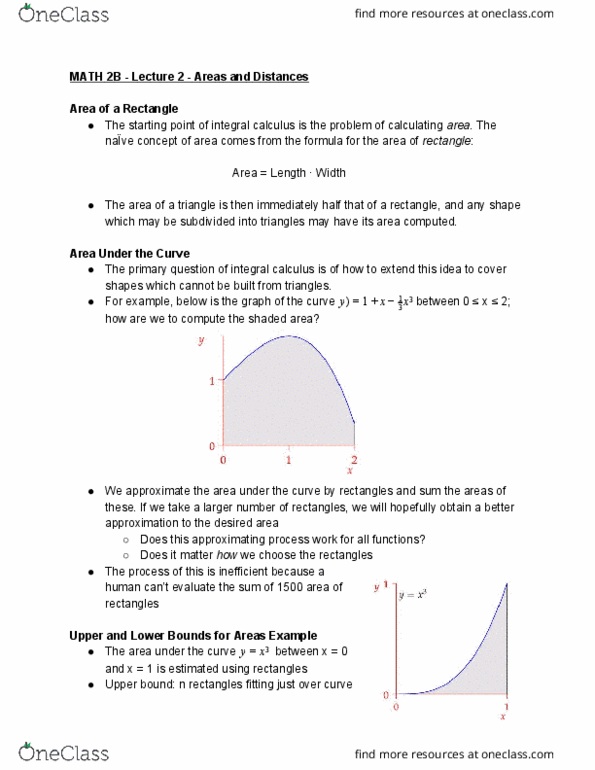
Math 2b - lecture 2 - areas and distances. The starting point of integral calculus is the problem of calculating area . The na ve concept of area comes from the formula for the area of rectangle : The area of a triangle is then immediately half that of a rectangle, and any shape which may be subdivided into triangles may have its area computed. The primary question of integral calculus is of how to extend this idea to cover shapes which cannot be built from triangles. For example, below is the graph of the curve how are we to compute the shaded area? y = 1 + x 3. 1 3 x between 0 x 2; We approximate the area under the curve by rectangles and sum the areas of these. If we take a larger number of rectangles, we will hopefully obtain a better approximation to the desired area. Does it matter how we choose the rectangles.