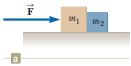
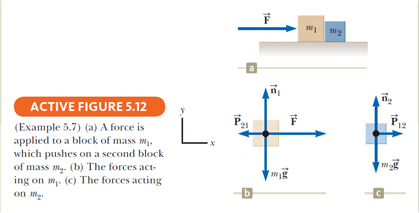
<p>A Simple Atwood Machine consists of two masses m1 and m1 that are connected by a string wound over a pulley, as seen in the figure below. m2 is larger than m1.<br />On a piece of paper, draw two free body diagrams; one for each of the masses, showing all forces acting on each mass. Then answer the following questions.<br /><br /><br />(a) Based on your free body diagram, identify the forces acting on the mass m1. Select all that apply.<br />(m1+m2)a<br />m1g<br />FN<br />m1a<br />(m1+m2)g<br />m2a<br />f<br />m2g<br />T<br /><br /><br /><br />(b) Using the direction rosette indicate the direction for each of the forces acting on m1 that you identified in part (a). If any of the forces listed below is not applicable, enter NA.<br />m1a= <br />m2a= <br />m1g= <br />m2g= <br />(m1+m2)a= <br />(m1+m2)g= <br />f= <br />T= <br />FN= <br /><br />(c) Based on your free body diagram, identify the forces acting on the mass m2. Select all that apply.<br />T<br />(m1+m2)g<br />m2g<br />m1g<br />(m1+m2)a<br />m1a<br />m2a<br />f<br />FN<br /><br /><br /><br />(d) Using the direction rosette indicate the direction for each of the forces acting on m2 that you identified in part (c). If any of the forces listed below is not applicable, enter NA.<br />m1a= <br />m2a= <br />m1g= <br />m2g= <br />(m1+m2)a= <br />(m1+m2)g= <br />f= <br />T= <br />FN= <br /><br />(e) Write Newton's Second Law equation (in the form Fnet = ma) for m1 in the y-direction.<br />Use the first answer box for the left hand side (LHS) of the equation and the second answer box for the right hand side (RHS) of the equation.<br />It is important to use the correct signs for each of the forces. Motion in the upward direction is positive and motion in the downward direction is negative. (Use m1, g, a, and T as appropriate.)<br />LHS = <br />RHS = <br /><br />(f) Write Newton's Second Law equation (in the form Fnet = ma) for m2 in the y-direction.<br />Use the first answer box for the left hand side (LHS) of the equation and the second answer box for the right hand side (RHS) of the equation.<br />It is important to use the correct signs for each of the forces. Motion in the upward direction is positive and motion in the downward direction is negative.(Use m2, g, a, and T as appropriate.)<br />LHS = <br />RHS = <br /><br />(g) Use your answers from parts (e) and (f) to get an expression for the magnitude of the tension T. (Use m1, m2, and g as appropriate.)<br />magnitude of T = <br /><br />(h) Use your answers from parts (e), (f), and (g) to find the magnitude of a, the acceleration of the system. (Use m1, m2, and g as appropriate.)<br />magnitude of a = <br /><br />(i) In what direction will each mass accelerate.<br />For mass m1: <br />For mass m2: <br /><br />(j) Suppose m1 = 7 kg and m2 = 11 kg. What is the tension in the string? <br />T = <br /><br />(k) Suppose m1 = 7 kg and m2 = 11 kg. What is the value of the acceleration?<br />a = <br /><br />(l) Suppose that m2 starts from rest at a height of 5 m. Use the Kinematic Equations to determine how long it takes for m2 to hit the ground.</p>
<p>A Simple Atwood Machine consists of two masses m1 and m1 that are connected by a string wound over a pulley, as seen in the figure below. m2 is larger than m1.<br />On a piece of paper, draw two free body diagrams; one for each of the masses, showing all forces acting on each mass. Then answer the following questions.<br /><br /><br />(a) Based on your free body diagram, identify the forces acting on the mass m1. Select all that apply.<br />(m1+m2)a<br />m1g<br />FN<br />m1a<br />(m1+m2)g<br />m2a<br />f<br />m2g<br />T<br /><br /><br /><br />(b) Using the direction rosette indicate the direction for each of the forces acting on m1 that you identified in part (a). If any of the forces listed below is not applicable, enter NA.<br />m1a= <br />m2a= <br />m1g= <br />m2g= <br />(m1+m2)a= <br />(m1+m2)g= <br />f= <br />T= <br />FN= <br /><br />(c) Based on your free body diagram, identify the forces acting on the mass m2. Select all that apply.<br />T<br />(m1+m2)g<br />m2g<br />m1g<br />(m1+m2)a<br />m1a<br />m2a<br />f<br />FN<br /><br /><br /><br />(d) Using the direction rosette indicate the direction for each of the forces acting on m2 that you identified in part (c). If any of the forces listed below is not applicable, enter NA.<br />m1a= <br />m2a= <br />m1g= <br />m2g= <br />(m1+m2)a= <br />(m1+m2)g= <br />f= <br />T= <br />FN= <br /><br />(e) Write Newton's Second Law equation (in the form Fnet = ma) for m1 in the y-direction.<br />Use the first answer box for the left hand side (LHS) of the equation and the second answer box for the right hand side (RHS) of the equation.<br />It is important to use the correct signs for each of the forces. Motion in the upward direction is positive and motion in the downward direction is negative. (Use m1, g, a, and T as appropriate.)<br />LHS = <br />RHS = <br /><br />(f) Write Newton's Second Law equation (in the form Fnet = ma) for m2 in the y-direction.<br />Use the first answer box for the left hand side (LHS) of the equation and the second answer box for the right hand side (RHS) of the equation.<br />It is important to use the correct signs for each of the forces. Motion in the upward direction is positive and motion in the downward direction is negative.(Use m2, g, a, and T as appropriate.)<br />LHS = <br />RHS = <br /><br />(g) Use your answers from parts (e) and (f) to get an expression for the magnitude of the tension T. (Use m1, m2, and g as appropriate.)<br />magnitude of T = <br /><br />(h) Use your answers from parts (e), (f), and (g) to find the magnitude of a, the acceleration of the system. (Use m1, m2, and g as appropriate.)<br />magnitude of a = <br /><br />(i) In what direction will each mass accelerate.<br />For mass m1: <br />For mass m2: <br /><br />(j) Suppose m1 = 7 kg and m2 = 11 kg. What is the tension in the string? <br />T = <br /><br />(k) Suppose m1 = 7 kg and m2 = 11 kg. What is the value of the acceleration?<br />a = <br /><br />(l) Suppose that m2 starts from rest at a height of 5 m. Use the Kinematic Equations to determine how long it takes for m2 to hit the ground.</p>