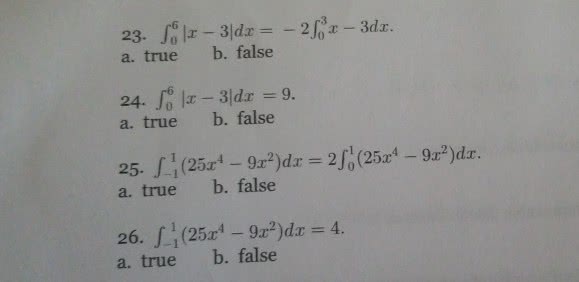🏷️ LIMITED TIME OFFER: GET 20% OFF GRADE+ YEARLY SUBSCRIPTION →
Log in
laisammamathew17

laisammamathew17

Lv2

0 Followers
0 Following
1 Helped

ANSWERS

Published27

Subjects

Prealgebra6Algebra12Probability1Geometry4Calculus3Mathematics1
Answer: -6bl+1+4b=-3b+6 -6b+4b+3b=6-1 -6b+7b=5 b=5
Share
Answer: All of them is true Explanation attached
Share
Answer: (V-3) ÷2=4÷3 V-3=(4/3) ×2 V-3=(4×2) ÷3 V=(8/3) +3 V=(8+9)/3 V=17/3 V=5...
Share

Look at the example! please.

Solve the system using elimination.
 
 
Select the correct choice below and fill in any answer boxes in your choice.
A. The solution is ___. (Type an ordered pair.)
B. There are infinitely many solutions.
C. There is no solution.
 
View an example I All parts showing
Solve the sythem wing ehifinanon.
 
 
 
We can eliminate x or y. Let's eliminate x. Consider the terms in x in each equation, that is, x and 2x. To eliminate x, we can multiply each term of the first equation to -2 then add the equations together.
The first equation, x + 5y = 7, becomes after multiplying it by -2, -2x - 10y = -14.
Because the coefficients of x in the two equations differ only in sign, add the two equations, eliminating the x-terms.
 
 
 
 
Now solve the nerw equation for y
-4y = -8 
y = 2
 
Finally, back-substitute 2 for y into one of the original equations to find x. We will use the first equation
x + 5y = 7            Ths is the first equation in for given system
x + 5 [2] = 7        Subtract 2 for y
x + 10 = 7            Multiply 
x = -3                   Subtract 1/0 from both sides. 
 
Using x = -3 and y = 2, we write the solution as an ordered pair (-3, 2)
Thus, x = -3 and y = 2. The proposed solution, (-3, 2), can be shown to satisfy both equations in the system. Consequently, the solution is (-3, 2)
Answer: explanation attached
Share
Solve the following systems of equations by elimination, if a solution exists.
 
Select the correct choice below and fill in any answer boxes in your choice.
A. The solution to the system is x=⬜, y=⬜ (Type integers or simplified fractions.)
B. There are infinitely many solutions.
C. There is no solution.
 
Solve the system using elimination.
 
We can eliminate x or y. Let's eliminate x Consider the terms in $x$ in each equation, that is, x and 2x. To eliminate x, we can multiply each term of the first equation by -2 then add the equations together,
The first equation, x+5 y=7, becomes after multiplying a by -2,-2 x-10 y=-14.
Because the coefficients of x in the two equations differ only in sign, add the two equations, eliminating the x-terms.
add
Now solve this new equation for y.
 
 
 
Answer: Explanation attached
Share
Solve the system of equations.
 
x+4 y-z=14 
x+5 y+z=27 
x-4 y+5 z=-2
 
Select the correct choice below and fill in any answer boxes within your choice.
A. The one solution is x = ___, y = ___, and z =___. (Simplify your answers.)
B. There are infinitely many solutions. If z is allowed to be any real number, then x =___ and y = ___ (Type expressions using z as the variable.)
C. There is no solution.
 
View an example I All parts showing
Solve the system of equations.
 
x+6 y-z=-19 
x+7 y+z=-18 
x-5 y+7 z=30
 
Use the left-to-right elimination method to solve this system of equations. This method reduces the system to an equivalent system in echelon form shown below, where a, b, c, d, e, and f are constants.
 
x + a y + bz = d 
         y + cz = e 
                 z = f
 
Note that the first equation, x + 6y - z = -19, is already in the form of the first row in echelon form.
 
The operations shown helom when perisemed on a system of equations, result in an equivalent system
1. Interchange any two equations.
2. Multiply both sides of the equations by the same nonzero number.
3. Multiply any equation by a rumber, add the result to a second equation, and then replace the second equation with the sum.
 
To eliminate the x-term from the second equation, multiply both sides of the first equation by -1 and ass the result to the second equation.
 
 
 
 
Now use the same method to eirinale the x-term in the third equation.
Multely beth sides of the first equation by -1 and add the result to the third equation.
 
 
The equation system with the nea second and third equation is shown below. The next step is to eliminate the yeterm from the thad equation.
 
x + 6y - z = 19 
      y + 2z = 1 
-11y + 8z = 49
 
To eliminate the y-term in the third equation, multiply both sides of the second equation by 11 and add the result to the third equation.
 
 
Finally, to obtain an x-coefficient of 1 in the third equation, multiply both sides of the third equation by .
 
 
The system is now in echelon form. Solve by back-substitution.
x + 6y - z = -19 
        y + 2z = 1 
                z = 2
 
The third equation gives the value of z.
Back-substitute 2 for z in the second equation and solve for y.
 
y + 2(2) = 1 
y = -3
 
Finally, back-substitute the values of y and z in the first equation and solve for x.
 
             x + 6 (-3) - (2) = -19 
                      x = 1    
 
Therefore, the solution to the given system is as shown below.
          x = 1               y = -3              z = 2
Answer: Explanation attached
Share
Explanation attached
Share
Answer: Glenda paid for 6books=$24 Glenda paid for 1book=24/6 =4 Therefore $4 ...
Share
Answer: 8×5=40 4×6=24 That is, 40-24=16 16+78=94
Share
Answer: 2×6=12 4+2+5+12=23
Share
Answer: 7×5=35 7×9=63 35+63=98 by bodmas rule
Share
Answer: X+5=10 X=10-5 X=5
Share
Answer: (X-3)and (x-2) Step-by-step explanation:Explanation attached
Share
Answer: Answer 0. 091Step-by-step explanation:Explanation attached
Share
Answer: loga+logb=logab That is, log(2x×3x×4x) =log20x log24x^3=log20x That is...
Share
log( 3+x) - log(x-4) =log2 log[(3+x) /(x-4) ] =log2 That is, (3+x)/(x-4)=2 3+x...
Share
Answer: Explanation attached
Share

Answer: ∆OTP is congruent to∆AZP using angle angle side Proof OT is congruent ...
Share

Answer: ∆ABC is congruent to ∆XYZ by side angle side theorem From the figure i...
Share

Images attached
Share

Answer: Here <A=<F And <Tis congruent to <P The sides AE is congru...
Share
Attached
Share
Answer is attached to it
Share
Sum of points scored by 6 games =21+15+16+19+9+25=105 Average of seven games=1...
Share
Answer:
Share
Answer: Step-by-step explanation
Share
Answer: Let 2x+5=0 2x=(-5) that is x=(-5/2) Therefore for (-5/2) the value doe...
Share

Weekly leaderboard

Start filling in the gaps now
Log in