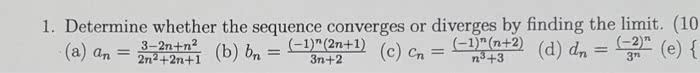MATH 1005 Study Guide - Ratio Test, Direct Comparison Test, Alternating Series Test

• School: Carleton University
• Department: Mathematics
• Course: MATH 1005
• Professor: Ida Toivonen

Document Summary

[5: determine whether the sequence converges or diverges. Solution: (a) lim n (cid:1) (b) lim n ( 4)n. 3n (cid:2) (cid:1) (d) (b) (cid:4)n (cid:3) (cid:4)n. 3 (cid:5)(cid:5)(cid:5)(cid:5) < 1 lim (cid:5)(cid:5)(cid:5)(cid:5) 1 (cid:5)(cid:5)(cid:5)(cid:5) 2 (cid:5)(cid:5)(cid:5)(cid:5) < 1. (cid:5)(cid:5)(cid:5)(cid:5) > 1. (cid:5)(cid:5)(cid:5)(cid:5) 4. 3 diverges since (cid:1) (cid:2) n2 en (e) (cid:2) (cid:4)n. 2 x2 ex = lim x n2 en = 0. [9] (d) the sequence diverges because (e) by l"h opital"s rule, lim x : find the sum of the series. 3: determine whether the series converges or diverges. (cid:6) (a) the function f(x) = (cid:7) and. 2 x[ln(x)]3 is continuous, positive, and decreasing for x 3, Hence, the series diverges by the nth-term test. (c) 1 n3/2 converges (p-series with p > 1), the. [12: determine whether the series converges absolutely, converges conditionally, or diverges. (cid:6) (d) n=0 ( 1)n(2n + 1)n (n3 + 1)n/2. 1 ln(n) is positive and decreasing, and lim n bn = 0.