MATH 111 Study Guide - Natural Number, Distributive Property, Rational Number
2 Jun 2012
School
Department
Course
Professor
Document Summary
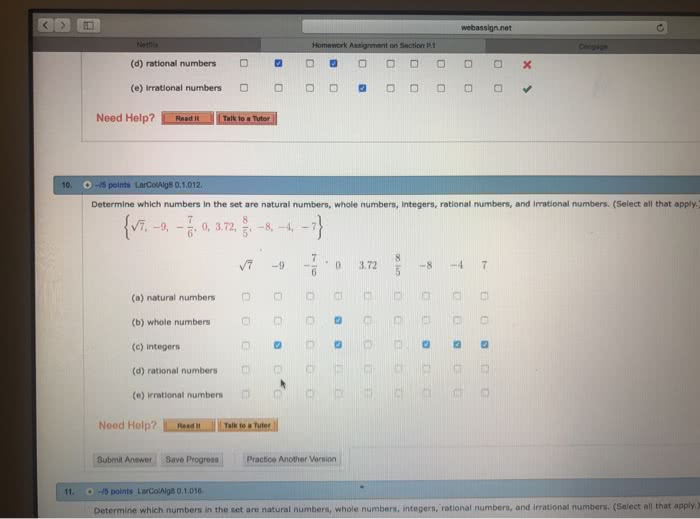
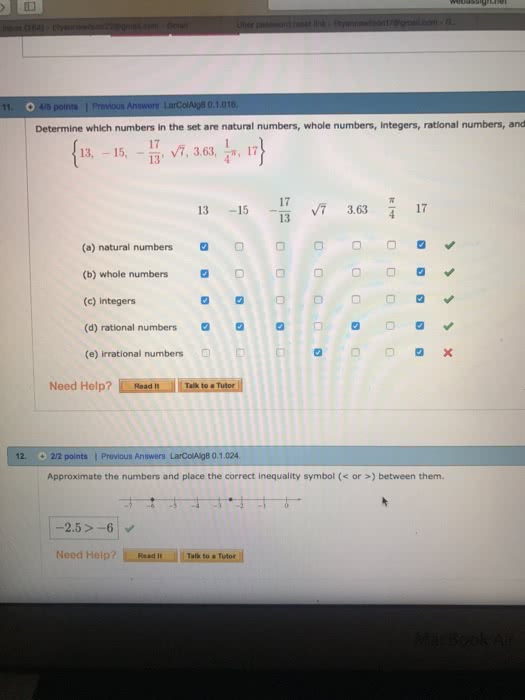
5. 1 the set or rational numbers rational numbers: q = {a/b | a and b are integers, and b 0}; ie/ fractions proper fraction: a/b where 0 a < b; if not, it is an improper fraction. 5. 1. 1 equivalent or equal fractions fundamental law of fractions: let a/b be any fraction and n a nonzero integer. then a/b = an/bn. 5. 1. 3 equality of fractions equality of fractions: two fractions a/b and c/d are equal if, and only is, ad = bc. 5. 2 addition, subtraction, and estimation with rational numbers. 5. 2. 2 mixed numbers mixed number: number made up of an integer and a proper fraction sometimes inferred 2 means 2 times since xy means x times y, but this is not correct. 2 means (2 + ) or equivalently -2 but not -2 + . 5. 2. 4 subtraction of rational numbers subtraction of rational numbers in terms of addition: if a/b and c/d are any rational numbers, then a/b.
