🏷️ LIMITED TIME OFFER: GET 20% OFF GRADE+ YEARLY SUBSCRIPTION →

HomeStudy Guides420,000CA160,000

MTHE 225 Quiz: quiz 6 (10).pdf

102 views2 pages

rosereindeer362

20 Nov 2012

School

Queen's University

Department

Mathematics & Engineering Courses

Course

Professor

Gregory G Smith

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

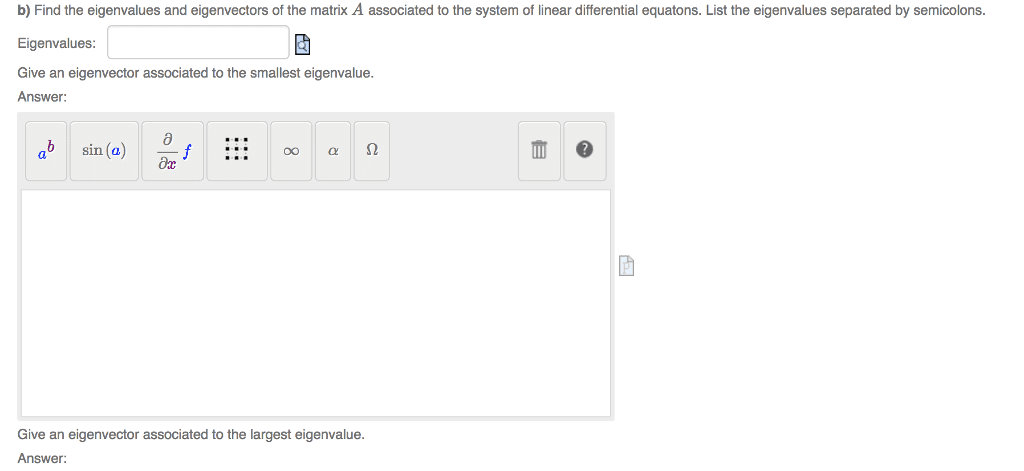
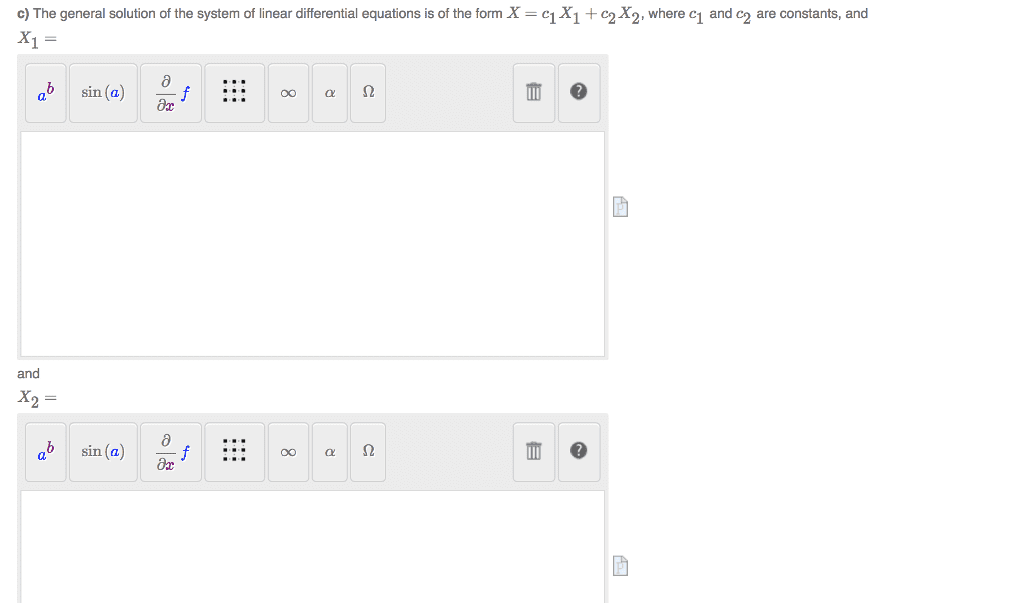
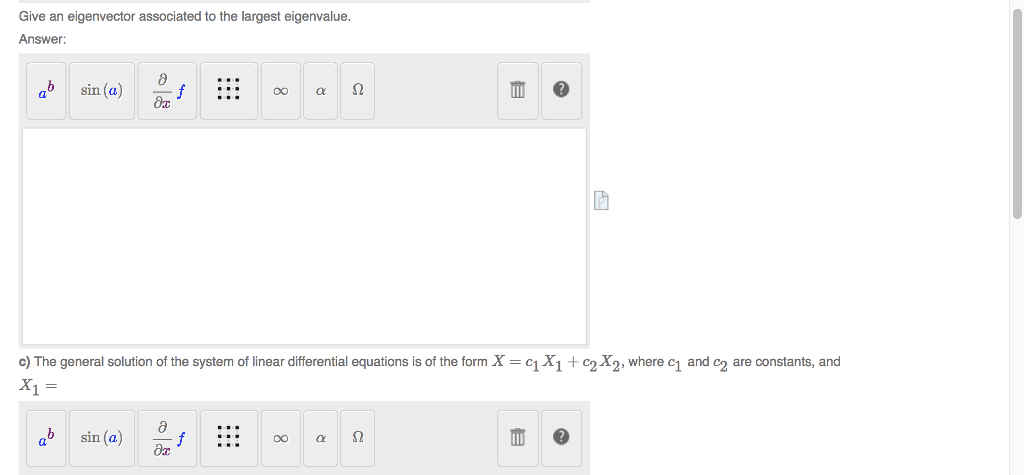
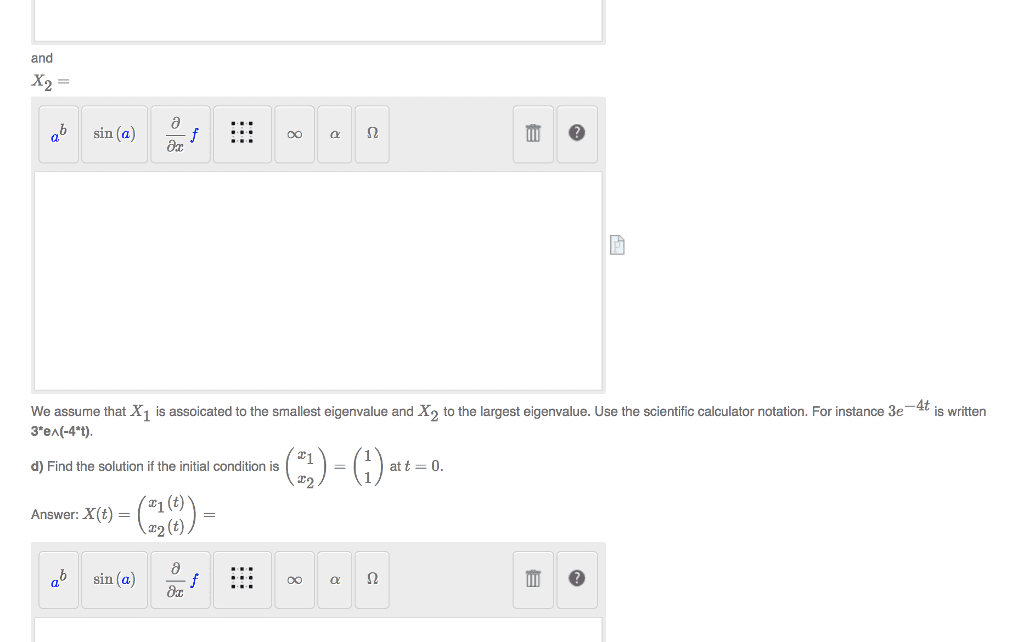
We are asked to use the eigenvalue method to nd a solution to the following linear system, satisfying the speci ed initial conditions. x . 2 = 6x1 2x2 , x1(0) = 1 , x2(0) = 0. 6 2! has eigenvalues = 3, = 4, as is seen from the characteristic. 5 polynomial: det(a i) = det 9 . To nd the eigenvector v corresponding to = 3, we solve the system. To nd the eigenvector v corresponding to = 4, we solve the system. Thus the two independent solutions are to nd v = 1 x1(t) = e3t 5. 1 and so the general solution is x(t) = c1e3t 5. E4t! c1 c2! x(t) = x(t)c = 5e3t c2! such that. Now we wish to nd c = c1 which can be written as. We nd c1 = 1, c2 = 6, thus or. 1! x1(t) = 5e3t + 6e4t x2(t) = 6e3t.

Related Documents

MATH 4389 Study Guide - Final Guide: Diagonal Matrix, Invertible Matrix, Diagonalizable Matrix

Applied Mathematics 1411A/B Lecture Notes - Lecture 17: Row And Column Vectors, Main Diagonal, Triangular Matrix

Applied Mathematics 1411A/B Lecture Notes - Lecture 17: Elementary Matrix, Triangular Matrix, Row And Column Vectors

Related Questions

Show transcribed image text

Show transcribed image text

harlequinserval672

For the best rating please complete by answering all thequestions in one post so I could rate you once you post.

Answers must be correct in order to get best rating.

1. Factor out the GCF from thepolynomial.
20m^9 + 6m^7 + 20m^5

2(10m^9 + 3m^7 +10m^5)
No common factor
m^5 (20m^4 + 6m^2 +20)
2m^5 (10m^4 + 3m^2 +10)

2. Find the solution to the system by addition(elimination) method.
4x + 15y = 15
8x - 3y = -3

(1, 0)
(0, 0)
(0, 1)
(1, 1)

3. (11p + 4)(11p - 4)

p^2 - 16
121p^2 + 88p - 16
121p^2 - 16
121p^2 - 88p -16

4. Find the solution to the system by addition(elimination) method.
2x + 15y = -91
9x + 5y = 28

(-5, 7)
(7, -7)
(9, -9)
(-7, 7)

5. Factor by grouping.
18x^3 + 15x^2 + 12x + 10

(3x^2 + 2)(6x + 5)
(18x^2 - 2)(x - 5)
(3x^2 - 2)(6x - 5)
x(18x + 2)(x +5)

6. (x + 3y)(x + 5y)

x^2 + 5xy + 15y^2
x^2 + 8xy + 8y^2
x^2 + 8xy + 15y^2
x + 8xy + 15y

7. 6x^7 (9x^7 + 12x^2 - 7)

54x^7 + 72x^2 - 42
54x^14 + 72x^9
54x^14 + 72x^9 -42x^7
54x^14 + 12x^2 -7

8. 15x^2 - 12x + 10x - 8

(15x + 2)(x - 4)
(15x - 2)(x + 4)
(3x - 2)(5x + 4)
(3x + 2)(5x -4)

9. For the polynomial, state the degree andwhether or not the polynomial is a monomial, a binomial, or atrinomial.
5x^3y^4 - 8x^5y^6 + 8

Binomial, degree 7
Trinomial, degree 3
Trinomial, degree18
Trinomial, degree11

10. (3x^8 + 2x^7 - 4x^6 + 8) + (7x^8 - 4x^7 +8x^6 + 1)

10x^8 - 2x^7 + 4x^6 +9
12x^42 + 9
10x^26 - 2x^14 + 4x^12 +9
4x^8 + 4x^7 + 4x^6 +9

11. (2n^5 - 3n^3 - 6) - (5n^5 - 14n^3 -3)

-3n^5 + 2n^3 - 9
-3n^5 + 11n^3 - 3
5n^8
-3n^5 + 11n^3 -9

12. Use the substitution method to solve thesystem.
x - 4y = -13
7x - 5y = -22

(1, 4)
(-2, 4)
(-1, 3)
No solution

13. Use the substitution method to solve thesystem.
8x - 6y = 32
2x - 2y = 8

(3, 1)
(4, 1)
(4, 0)
No solution

14. Terms in a polynomial are separated byaddition or subtraction.

15. A polynomial is an algebraic expression ofone or more terms.

16. A solution of two linear equations in twovariables is an ordered pair that is a solution to eachequation.

17. The greatest common factor will always begreater than the largest factor of each term of theexpression.

18. A system of equations in two variables mayhave infinite solutions.

19. When two or more algebraic expressions aremultiplied, each expression is called a term.

20. Factoring is multiplication inreverse.