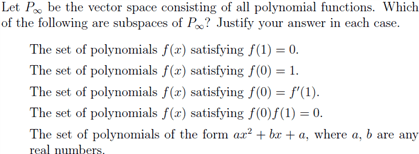MATH 308 Study Guide - Final Guide: Feasible Region, Linear Programming, Yottabyte
1 Dec 2011
School
Department
Course
Professor
Document Summary
These notes are a supplement and summary to the textbook for math 308. Students are expected to know this material for the nal examination. Here is the missing proof of theorem 13, page 13: convexity of feasible regions. Let h rn be a closed half-space consisting of those points x = (x1, x2, . , xn) satisfying the inequality a1x1 + a2x2 + + anxn b. , xn) and y = (y1, y2, . , yn) belong to h, and let t satisfy 0 t 1. This last inequality states that the point tx + (1 t)y belongs to h, as required. (cid:3) The intersection of two convex sets is convex. Suppose that s and s are convex sets, and that x and y belong to s s . Since s is convex, then tx + (1 t)y s. since s is convex, then tx + (1 t)y s . Therefore tx + (1 t)y s s .
