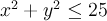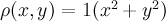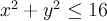MATH209 Study Guide - Multiple Integral, Standard Deviation, Hypotenuse
14 Nov 2013
School
Department
Course
Professor
Document Summary
A similar application would be for electric charge over a region d. if the charge density (units of charge/unit area) is given by (x, y) at a point (x, y) in d, then the total charge q is: Example 1: charge is distributed over the triangular region d bounded by y = 1-x, x = 1, y = 1 and the charge density at (x, y) is (x, y) = xy, measured in. Recall: the moment of a particle about an axis is the product of its mass and its directed distance from the axis. So to get the moment of a lamina about the x-axis: Similarly, the moment of a lamina about the y-axis: The center of mass is the point (x*, y*) such that mx* = my and my* = mx. In other words, the lamina behaves as if its entire mass is concentrated at its center of mass.
