MATH117 Study Guide - Radian, Asparagine, Quotient Rule

• School: University of Waterloo
• Department: Mathematics
• Course: MATH117
• Professor: Eddie Dupont

Document Summary

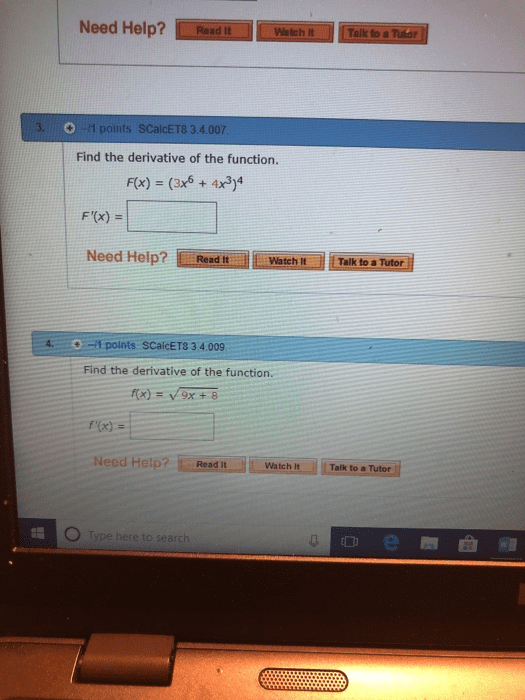
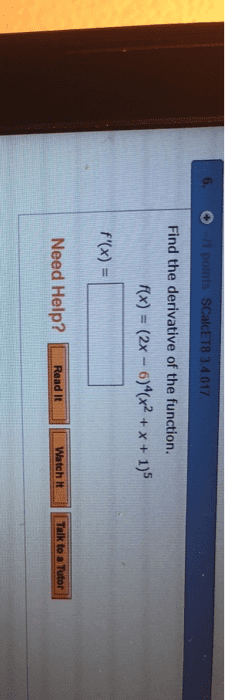
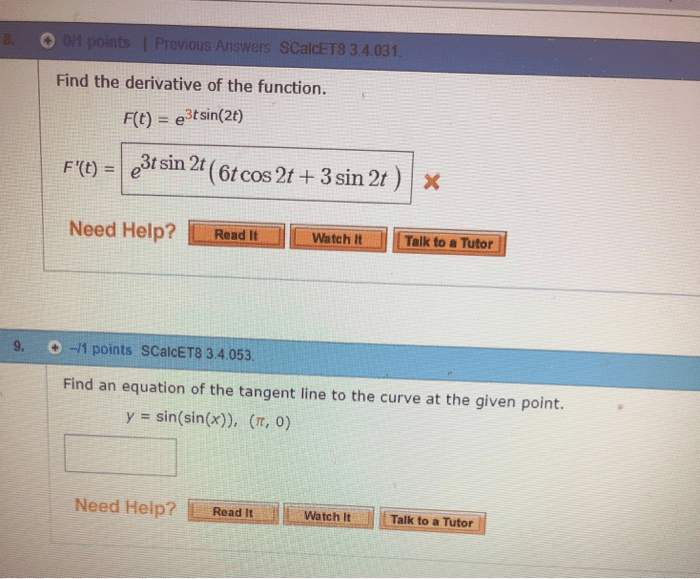
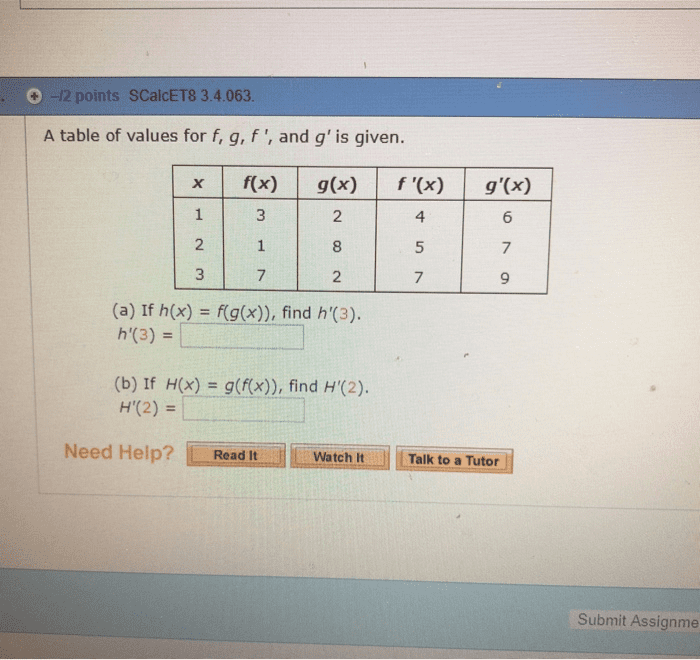
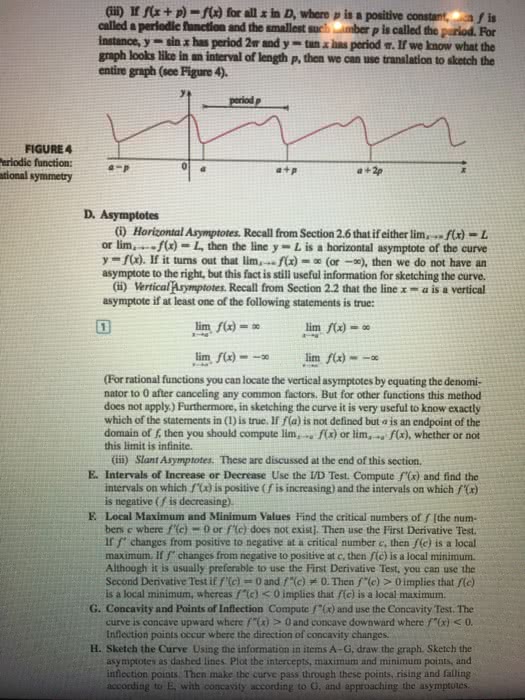
A function is a rule which assigns a single output to a variable given at least one input variable. In this class we deal only with a single input x and write y = f(x: x is the indepenant variable, y is the dependant variable. A domain is the set of allowable values for the independant variable (x) A range is the set of possible values for the dependant variable (y) If y = f (x) and x = g(t) then we can view y as a function of t, y = f (g(t)), which we sometimes write as y = f g(t) For f (x) = 1 sin x, g(x) = x3, f g(x) = f (x3) = 1 sin x3 g f (x) = g(1 sin x) = (1 sin x)3. R = {y | y = f g(x), x dg} or. R = {y | y = f (x), x rg}