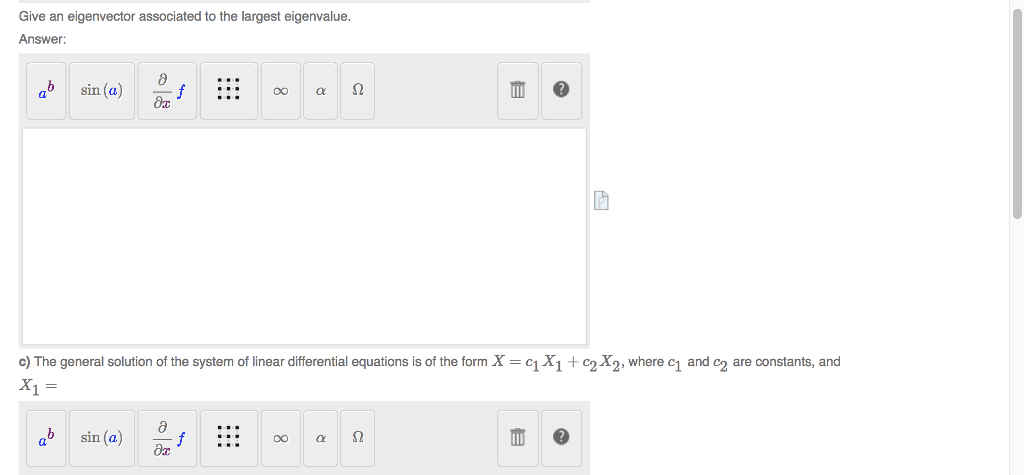
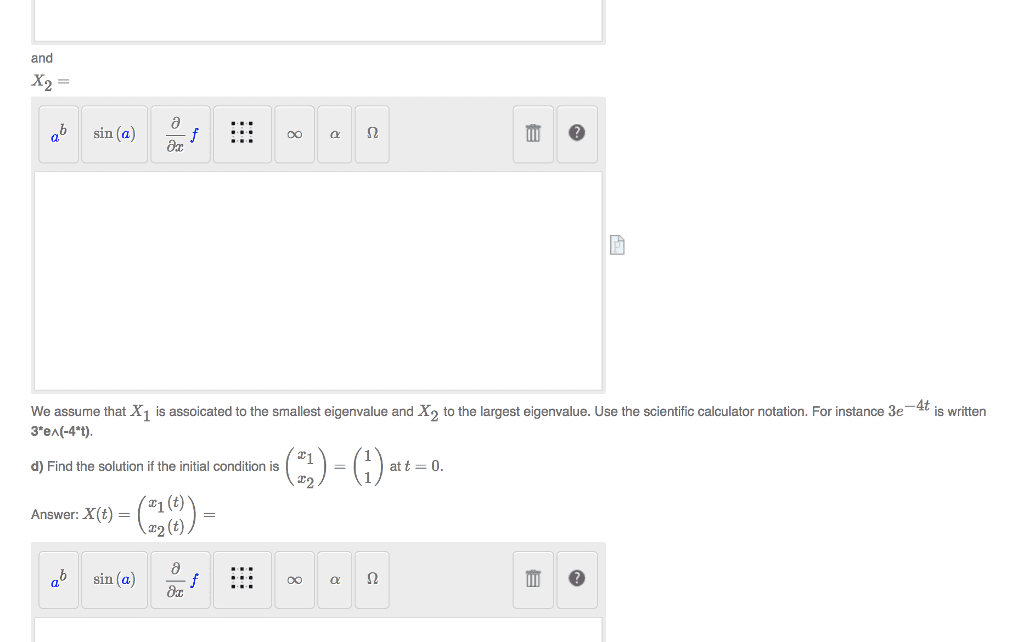
MATH136 Study Guide - Tx1, Spanx, Symmetric Matrix

• School: University of Waterloo
• Department: Mathematics
• Course: MATH136
• Professor: Robert Sproule

Document Summary

Monday, march 31 lecture 34 : more on eigenvectors. Concepts: recognize that 1 is an eigenvalue of a if and only if 1/ 1 is an eigenvalue of a-1, define algebraic and geometric multiplicity of an eigenvalue. 34. 1 proposition let a be an invertible matrix. If 1 is an eigenvalue of a then 1/ 1 is an eigenvalue of a 1 . Furthermore, x1 is an eigenvector associated to 1/ 1 if and only if x1 is an eigenvector of 1 . Then a does not have an eigenvalue equal to zero since (a 0i)x = ax = 0 only has the trivial solution (since a is invertible). The matrix equation ax = 1x has a non-trivial solution x1. Ax1 = 1x1 for some non-zero eigenvector. A 1x = (1/ 1)x has a non-trivial solution. 1/ 1 is an eigenvalue of a 1with x1 as an eigenvector.