MATH137 Final: Mean Value Theorem, MVT Examples

36
MATH137 Full Course Notes
Verified Note
36 documents
Document Summary
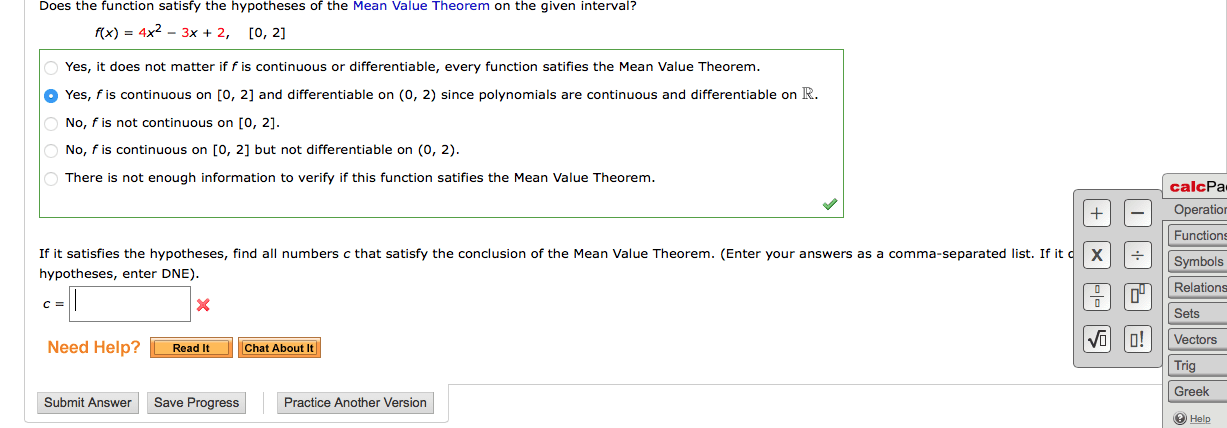
Lec 22 - the mean value theorem (mvt) Let be a function that satisfies 3 hypotheses: 3. is continuous on (a closed interval) is differentiable on (an open interval) Screen clipping taken: 11/2/2011 11:49 am b) c) d) Case 1: a constant (figure a) so could be any number in . Case 2: for some in (figure b and d) By the evt (which applies because of hypothesis 1), attains its max value on. So has a local max at , and is differentiable at (by hypothesis 2 since ) Case 3: for some (figure c and d). By the evt (which applies because of hypothesis 1), attains its min value on. So has a local min at , and is differentiable at (by hypothesis 2 since ) Let be a function that satisfies the 2 hypothesis: = slope of secant from (a, f(a)) to (b, f(b))