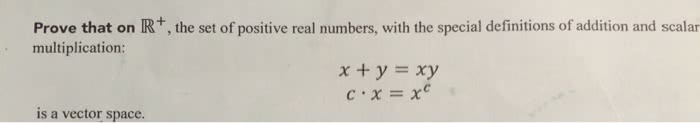MATH235 : lect136_3_w14.pdf
Document Summary
Friday, january 10 lecture 3 : spans and subspaces of n: lines and planes which are subspaces in 3, determining if a subset is a subspace of n, basis of a subspace, standard basis of n. 3. 1 introduction up to now we have referred to the elements of the set n as vectors. For reasons which we will make clear later we will now refer to n not simply as the set. 3 we will say the vector space 3. This means that, if v and w belong to w then so does v + w for any scalars and . Note: the word equivalently means that w is closed under scalar multiplication closed under addition if and only if w is closed under linear combinations : w is closed under scalar multiplication and closed under addition . This of all n-tuples of real numbers but as a vector space. For example, rather than say the set satisfies two conditions.