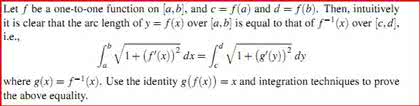MAT102H5 Study Guide - Quiz Guide: Multiplication Table

• School: UTM
• Department: Mathematics
• Course: MAT102H5
• Professor: Shay Fuchs

Document Summary

Let a, b two nonempty sets and f : a b a function: [2 marks] prove that for any two subsets c a and d a, we have f(c d) f(c) f(d). Solution: suppose that y f(c d). Then y = f(x) for some x c d. since x c, we have that y f(c) and since x d, we have that y f(d). Find two subsets c, d of a for which f(c) f(d) = {x, y} and f(c d) = {x}. Solution: let c = {1, 2} and d = {2, 3}. Then f(c) = {x, y} and f(d) = {x, y}, so that f(c) f(d) = {x, y}. Since c d = {2}, we have f(c d) = {f(2)} = {x}. Note: this example shows that that the inclusion in part a) of the question need not be an equality.