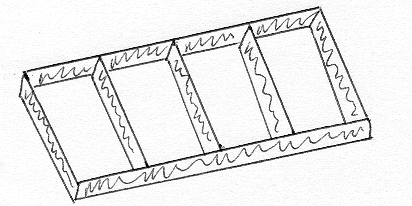
MAT 137Y, 2007–2008 Winter Session – Solutions to Term Test 2
(15%) 1. A farmer with 1500 feet of fencing wants to enclose a rectangular area and then divide it into four
pens (fenced enclosures) with fencing parallel to one side of the rectangle. Find the largest possible
total area of the four pens; be sure to verify that the area is indeed maximized.
Draw a diagram. Let xbe the length of the side of the field with the five parallel fences. The amount
of fencing used is therefore 5x+2y=1500. We are asked to maximize the rectangular area, that is,
A=xy =x(750 −5
2x), where xmust be between 0 and 300. To do this, we find A0:
A(x) = 750x−5
2x2=⇒A0(x) = 750 −5x=0=⇒x=150.
At the endpoints, A=0, so the critical point must yield the maximum area, hence the largest possible
area is 150 ·375 =56250 square feet.
2.
(10%) (i) Find the values of aand bsuch that lim
x→0
sin2x+ax3+bx
x3=0.
Let Lbe the limit above. The numerator and denominator both go to zero, so by L’Hˆ
opital’s
Rule,
L=lim
x→0
2cos2x+3ax2+b
3x2.
Since the denominator of the new limit goes to zero, the limit exists only if the numerator goes
to zero. Therefore, b=−2. Applying L’Hˆ
opital’s Rule again twice gives us
L=lim
x→0−4sin 2x+6ax
6x=lim
x→0−8cos 2x+6a
6=0,
which is true when a=4
3. Hence a=4
3and b=−2.
(10%) (ii) The length of a rectangle is increasing at a rate of 7 cm/sec and the width is decreasing at 2
cm/sec. When the length is 20 cm and the width is 6 cm, determine whether the area of the
rectangle is increasing or decreasing, and find the rate at which the area is changing.
Let lbe the length and wbe the width. The area of the rectangle is A=lw, so
dA
dt =l·dw
dt +w·dl
dt .
When l=20 and w=6, we have dl
dt =7 and dw
dt =−2, so
dA
dt =20 ·(−2) + 6·7=2,
so the area is increasing at a rate of 2 square cm per second.
3. Let f(x) = 2√x−x.
(5%) (a) Find the domain of f(x)and, if any, the intercepts and asymptotes.
The domain is all x≥0. Intercepts occur at (0,0)and when
2√x−x=0=⇒2√x=x=⇒4x−x2=0=⇒x=0,4,
so (4,0)is a y-intercept. As the function is defined for all values of x≥0 and lim
x→0−f(x) = 0 and
lim
x→∞
f(x) = −∞, there are no asymptotes.
1