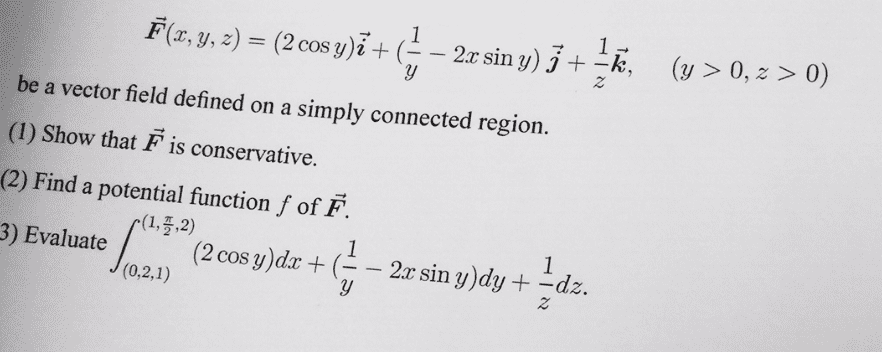MAT237Y1 Study Guide - Piecewise, Simply Connected Space, Iterated Integral
Document Summary
2( (i) show that f is conservative on. Hence f is conservative iff k z z. 3r , and of course which actually is the case. 0 (ii) find the potential function for f i. e. a scalar function f such that. 2 y f f f z y x zyxf implies. We may write for we get the point. F: [10 marks] verify the divergence theorem in case zyx y. 2 region in the first octant bounded by the plane. 2 x z i x j z and v is the. The boundary s of v consists of four faces smooth). 0zs dsnf dsnf dsnf dsnf zx zx ds plane. If you do not use the formula for the volume, you have to evaluate the iterated integral dv)001( hb. 0s: (a) [2 marks] let point x of s relative to. A point such that (b) [7 marks] evaluate. C t = is the interior point of s relative to.