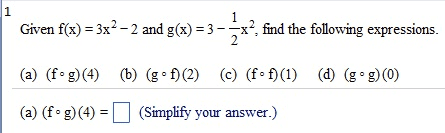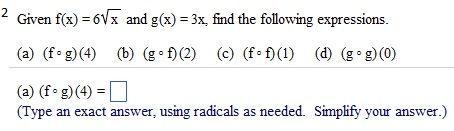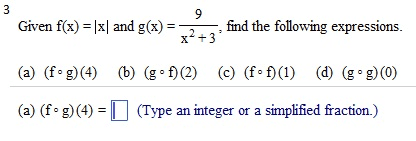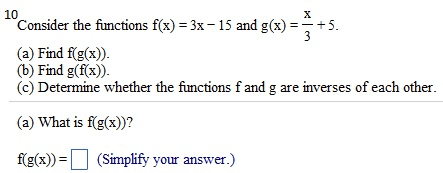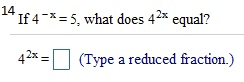Algebra
Please notice that some questions have multiple parts, i.e. a-cor a-d.
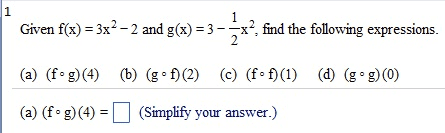
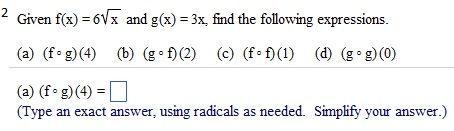
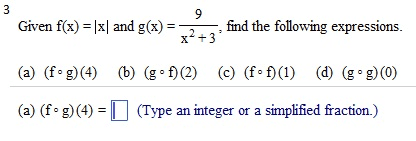


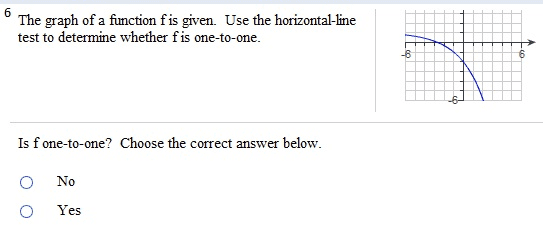



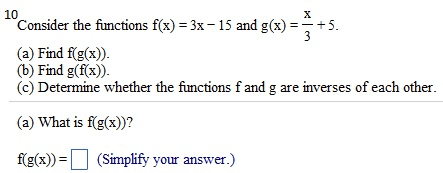

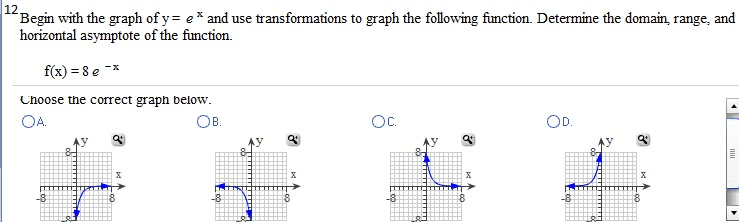

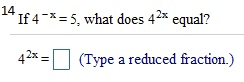
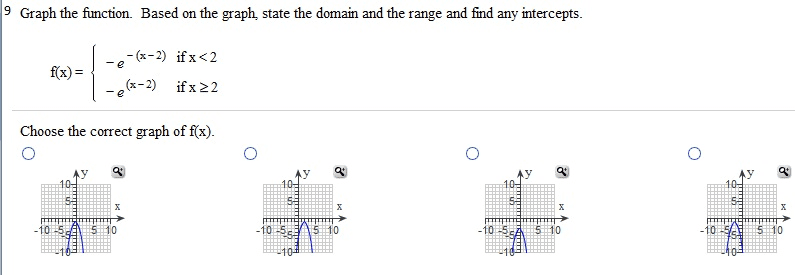
Given f(x) = 3x2 - 2 and g(x) = 3 - 1/2 x2: find the following expressions. (f.g)(4) (g f)(2) (f.f)(l) (g.g)(0) (f . g)(4) = (Simplify your answer.) find the following expressions, (f.g)(4) (g.f)(2) (f.f)(l) (g.g)(0) (fog)(4) = (Type an exact answer, using radicals as needed. Simplify your answer.) Given f(x) = |x| and g(x) =9/x2+3, find the following expressions. (f.g)(4) (g f)(2) (f.f)(l) (g.g)(0) (f . g)(4) = (Type an integer or a simplified fraction.) For the function on the right determine whether the function is one-to-one. Is the function one-to-one? Yes No For the function below, determine whether the function is one-to-one. {(7,7),(8,8),(9,46),(10,51)} Is the function one-to-one? Yes No For the function below, determine whether the function is one-to-one. {(7,7),(8,8),(9,46),(10,51)} Is the function one-to-one? Yes No The graph of a function f is given. Use the horizontal-line test to determine whether f is one-to-one. Is f one-to-one? Choose the correct answer below. No Yes The graph of a function f is given. Use the horizontal-line test to determine whether f is one-to-one. Is f one-to-one? Choose the correct answer below. No Yes Find the inverse of the one-to-one function. State the domain and range of the inverse function. {(10,-8), (-13,-10), (-9,2), (-8,11), (-10,1)} Which of the following is the inverse function? {(-10,1), (-8,11), (-9,2), (-13,- 10), (10,-8)} {(-8,10), (-10,-13), (2,-9), (11,-8), (1,-10)} {(-8,-10), (-10,-8), (2,-9), (11,-13), (1,10)} {(-10,8), (13,10), (9,-2), (8,-11), (10,-1)} Consider the functions f(x) = - 3x + 7 and g(x) = -1/3(x - 7). Find f(g(x)). Find g(f(x)). Determine whether the functions f and g are inverses of each other. What is f(g(x))? f(g(x)) = (Simplify your answer.) Consider the functions f(x) = 3x - 15 and g(x) = x/3 + 5. Find f(g(x)). Find g(f(x)) Determine whether the functions f and g are inverses of each other. What is f(g(x))? f(g(x)) = (Simplify your answer.) Match the graph to one of the following functions. y = 6x y = 6-x y = -6x y = -6-x y = 6x_ 1 y = 6x-1 Which function is represented by the graph? (Type A, B, C, D, E, F, G, or H.) Begin with the graph of y = ex and use transformations to graph the following function. Determine the domain, range, and horizontal asymptote of die function. f(x) = 8e-x Choose the correct graph below. Solve the equation. 4x.2x2=162 x = (Use a comma to separate answers as needed.) If 4-x = 5;what does 42x equal? 42x = (Type a reduced fraction.)
Show transcribed image text Given f(x) = 3x2 - 2 and g(x) = 3 - 1/2 x2: find the following expressions. (f.g)(4) (g f)(2) (f.f)(l) (g.g)(0) (f . g)(4) = (Simplify your answer.) find the following expressions, (f.g)(4) (g.f)(2) (f.f)(l) (g.g)(0) (fog)(4) = (Type an exact answer, using radicals as needed. Simplify your answer.) Given f(x) = |x| and g(x) =9/x2+3, find the following expressions. (f.g)(4) (g f)(2) (f.f)(l) (g.g)(0) (f . g)(4) = (Type an integer or a simplified fraction.) For the function on the right determine whether the function is one-to-one. Is the function one-to-one? Yes No For the function below, determine whether the function is one-to-one. {(7,7),(8,8),(9,46),(10,51)} Is the function one-to-one? Yes No For the function below, determine whether the function is one-to-one. {(7,7),(8,8),(9,46),(10,51)} Is the function one-to-one? Yes No The graph of a function f is given. Use the horizontal-line test to determine whether f is one-to-one. Is f one-to-one? Choose the correct answer below. No Yes The graph of a function f is given. Use the horizontal-line test to determine whether f is one-to-one. Is f one-to-one? Choose the correct answer below. No Yes Find the inverse of the one-to-one function. State the domain and range of the inverse function. {(10,-8), (-13,-10), (-9,2), (-8,11), (-10,1)} Which of the following is the inverse function? {(-10,1), (-8,11), (-9,2), (-13,- 10), (10,-8)} {(-8,10), (-10,-13), (2,-9), (11,-8), (1,-10)} {(-8,-10), (-10,-8), (2,-9), (11,-13), (1,10)} {(-10,8), (13,10), (9,-2), (8,-11), (10,-1)} Consider the functions f(x) = - 3x + 7 and g(x) = -1/3(x - 7). Find f(g(x)). Find g(f(x)). Determine whether the functions f and g are inverses of each other. What is f(g(x))? f(g(x)) = (Simplify your answer.) Consider the functions f(x) = 3x - 15 and g(x) = x/3 + 5. Find f(g(x)). Find g(f(x)) Determine whether the functions f and g are inverses of each other. What is f(g(x))? f(g(x)) = (Simplify your answer.) Match the graph to one of the following functions. y = 6x y = 6-x y = -6x y = -6-x y = 6x_ 1 y = 6x-1 Which function is represented by the graph? (Type A, B, C, D, E, F, G, or H.) Begin with the graph of y = ex and use transformations to graph the following function. Determine the domain, range, and horizontal asymptote of die function. f(x) = 8e-x Choose the correct graph below. Solve the equation. 4x.2x2=162 x = (Use a comma to separate answers as needed.) If 4-x = 5;what does 42x equal? 42x = (Type a reduced fraction.)