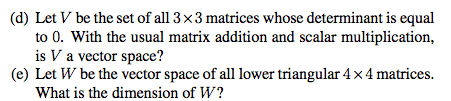MAT224H1 Final: Examples, Subspaces
Document Summary
M} is a subspace of k3 3 and nd its dimension. Problem: prove that the set of antisymmetric matrices {m k3 3|m t = Solution: to show w is a subspace we should verify these two conditions: if a, b w then a + b w, if k,a w then a w . If at = a and bt = b, then (a + b)t = at + bt = A b = (a + b), so a + b w: if at = a, then ( a)t = at = a so a w. To nd the dimension, we will nd a spanning set and show that it is linearly independent (or eliminate the dependent elements from it, if it turns out to be linearly dependent). According to the de nition of w , w = {(cid:16)a b c d e f. 1 0 0(cid:17), e3 = (cid:16)0 0 0.