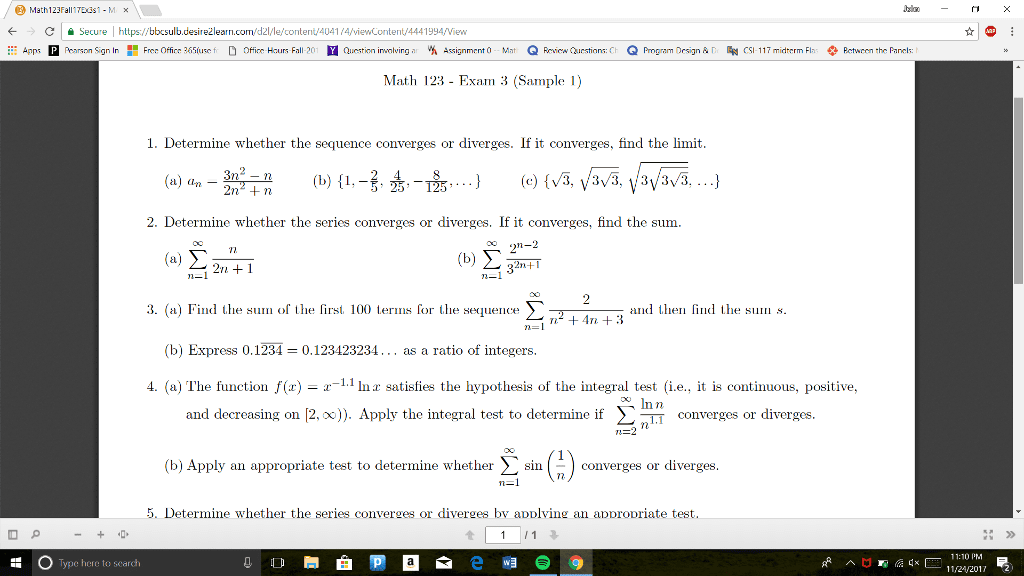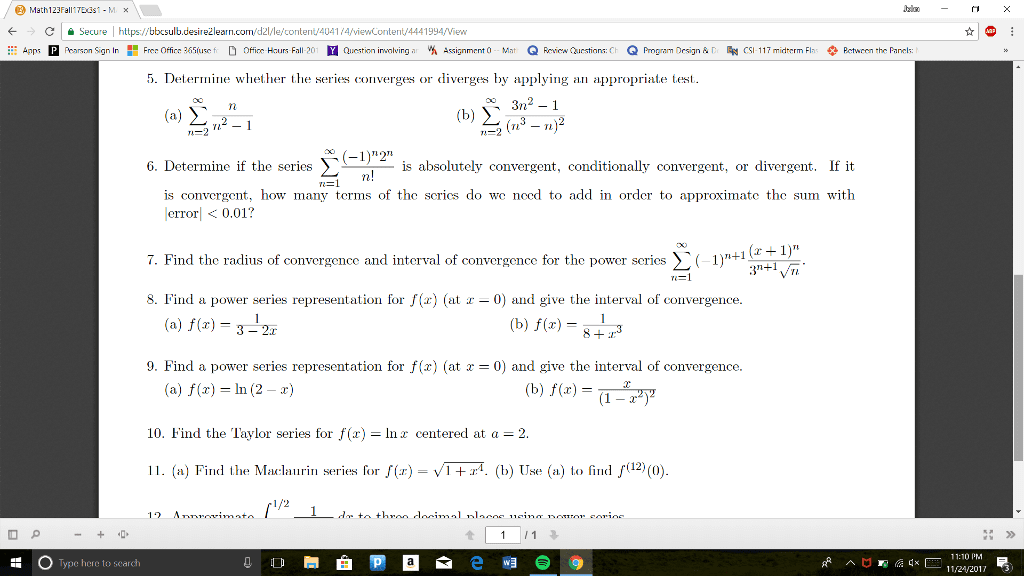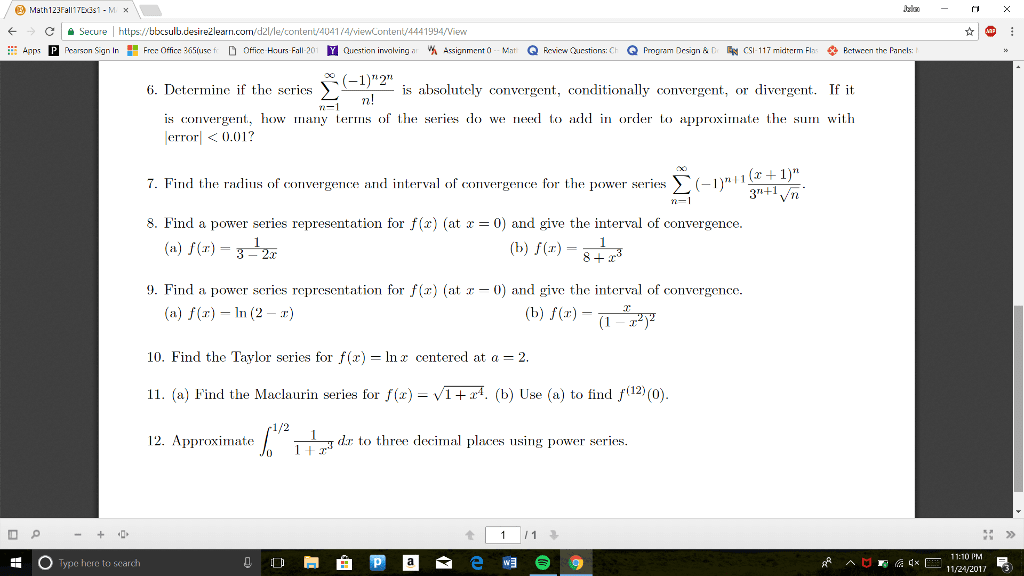Need help with this study guide for my calculus 2 midterm. Please solve problems and show the solutions step by step for each problem. 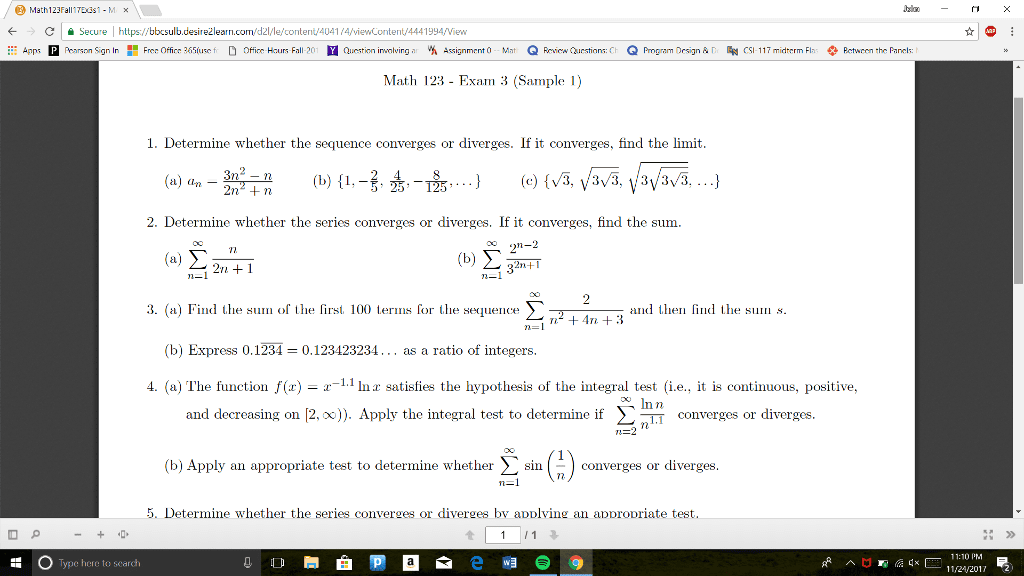
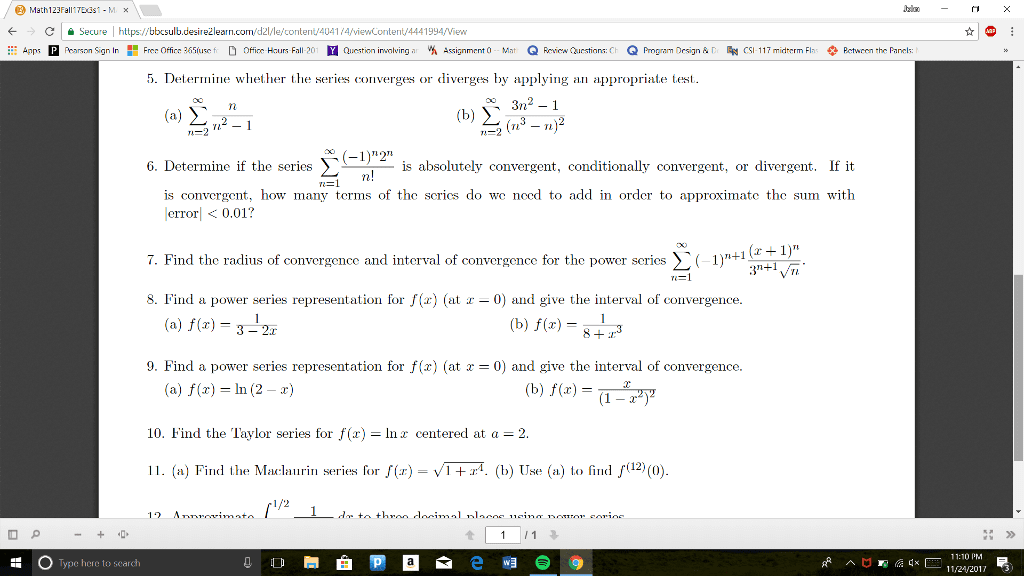
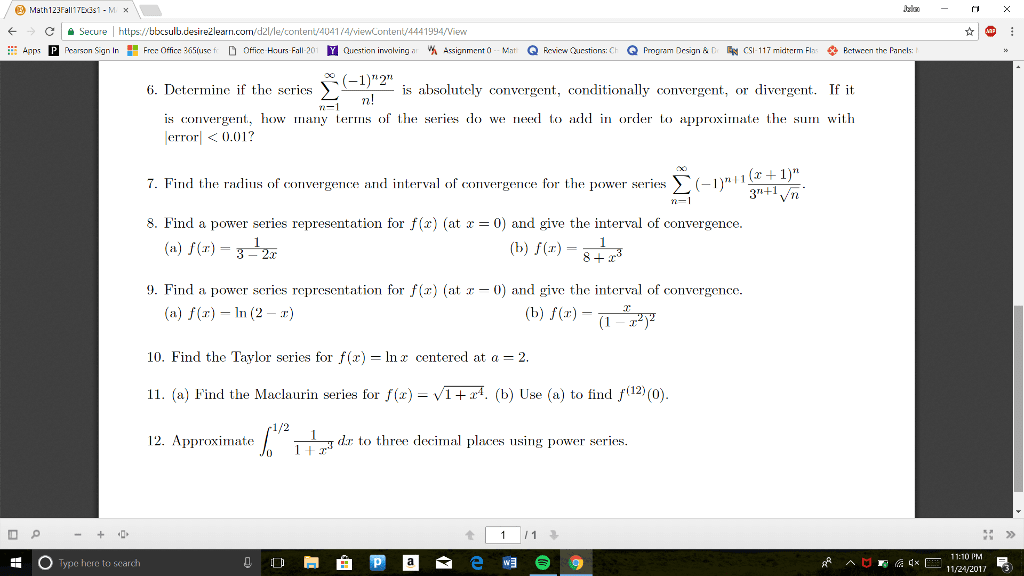 .
.
/ Math123FallTEast - MX Jalan - X e A Secure | https://bbcsulb.desirežlearn.com/dz//le/content/4041/4/viewcontent/4441994/View * @ : # Apps Pearson Sign In B Free Office 365(use fie D offices Hurs Fall-201 Y Question involving ar % Assignment (o -- Mat Q Fevica Cuestiors: CE Q Program Design &D CSI-117 midterm Flus Pctween the Panels: Math 123 - Exam 3 (Sample 1) 1. Determine whether the sequence converges or diverges. If it converges, find the limit. _ 3n - n (b) {1, -34-, ...} (e) {V3, V3/3, 3/3/3, ...} (a) on -2n + n 2. Determine whether the series converges or diverges. If it converges, find the sum. ( #1 () à 3. (a) Find the sum of the first 100 terms for the sequence I , and then find the sum s. Ln2 + 4n +3 n=1' (b) Express 0,1234 = 0.123423234... as a ratio of integers. 4. (a) The function f(x) = -1.1 Inx satisfies the hypothesis of the integral test (i.e., it is continuous, positive, and decreasing on [2, x)). Apply the integral test to determine if E converges or diverges. Sni. (b) Apply an appropriate test to determine whether converges or diverges. 5. Determine whether the series converges or diverges by applving an appropriate test. O P - + + 1 1 : 0 Type here to search Ñон в Ñезема оо : » Ramna g« E 11:10 PM = - 11/21/2012