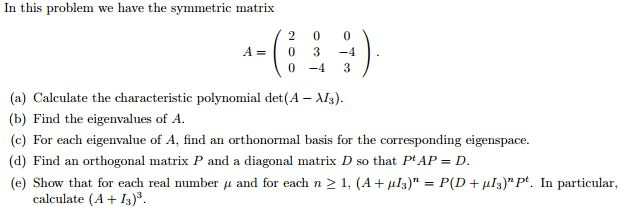MATH 2211 Midterm: Exam3210Sample3Ans
Document Summary
The properties of determinants: an n n matrix a is called orthogonal if aat = i. If a is orthogonal show that det(a) = 1. By the properties of determinant, det(aat) = det(a)det(at) = det(a)det(a) = det(a)2 = det(i) = 1. So, det(a) = 1: an n n matrix a is called skew-symmetric if at = a. Show that if a is skew-symmetric and n is an odd positive integer, then a is not invertible. By the properties of determinant, det(at) = det( a) det(a) = det( a) det(a) = ( 1)ndet(a) det(a) = det(a). So, we get det(a) = 0 which implies that a is not invertible. Every row of a is multiplied by -1. Find the volume of the parallelepiped with one vertex at the origin and adjacent vertices are (1, 0, 2), (1, 2, 4), and (7, 1, 0). 2 4 0 (cid:12)(cid:12)(cid:12)(cid:12)(cid:12)(cid:12) then take the absolute value to get the volume.