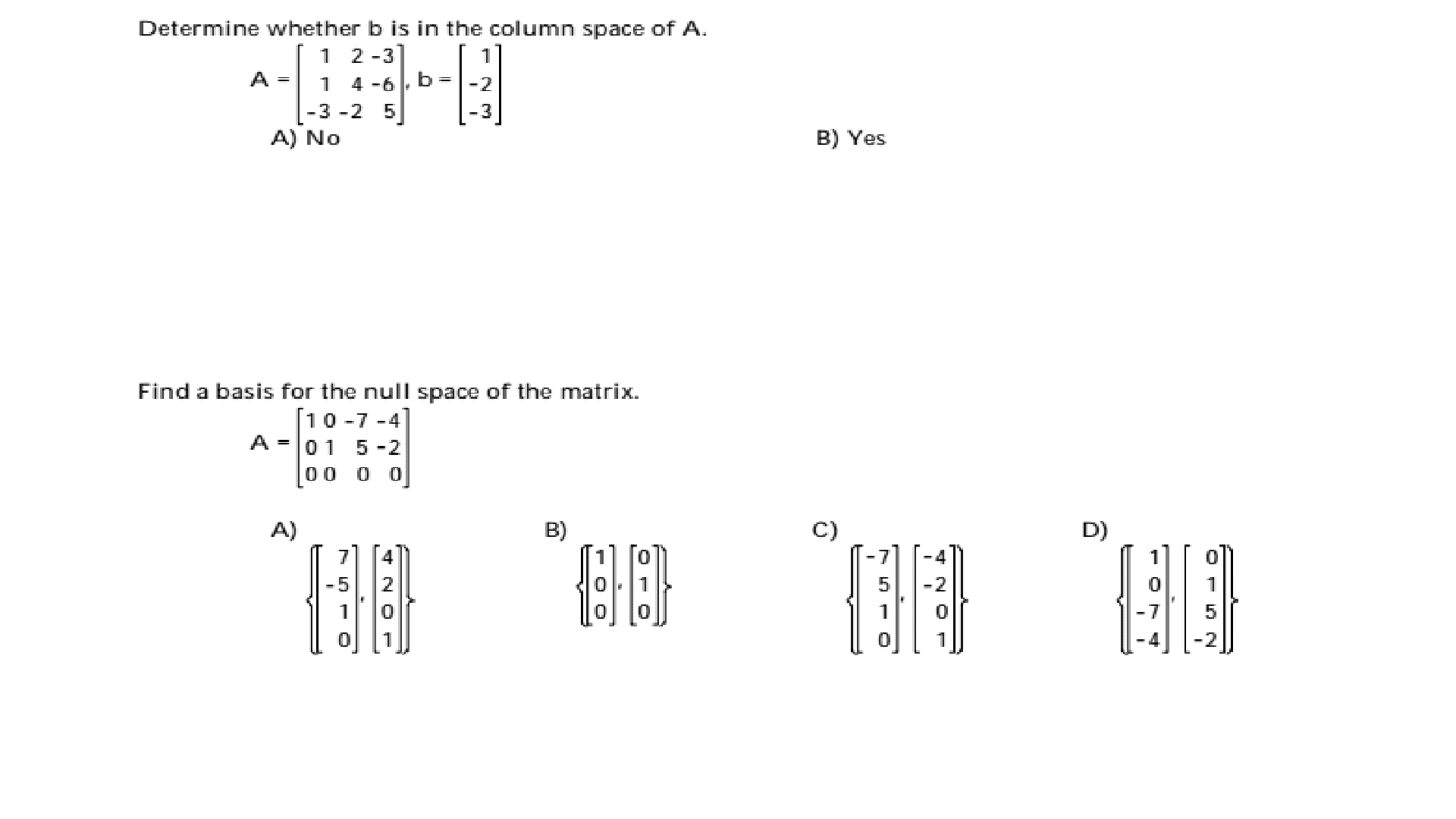
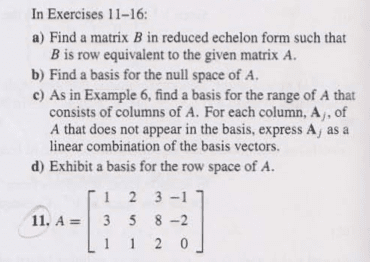MATH 2211 Quiz: Quiz8Spr11mt210Ans
Document Summary
Let a be the 4 5 matrix. 5: find the null space of a, find the column space of a, find a basis for the null space of a, find a basis for the column space of a. Before we answer the parts in the question, we need to reduce the given matrix. 0 (a) we need to solve ax = 0. Note that x1, x2, x3 are basic, x4 and x5 are free variables. : x4, x5 r which is a subspace of r5. (b) col a is the set of all linear combinations of the columns of a. 1 which is a subspace of r4. (c) notice that nul a is generated by 2 linearly independent vectors. 1 (c) notice that col a is generated by 5 vectors. But only the rst 3 of them are linearly independent.