APPM 2360 Midterm: appm2360spring2016exam3
Document Summary
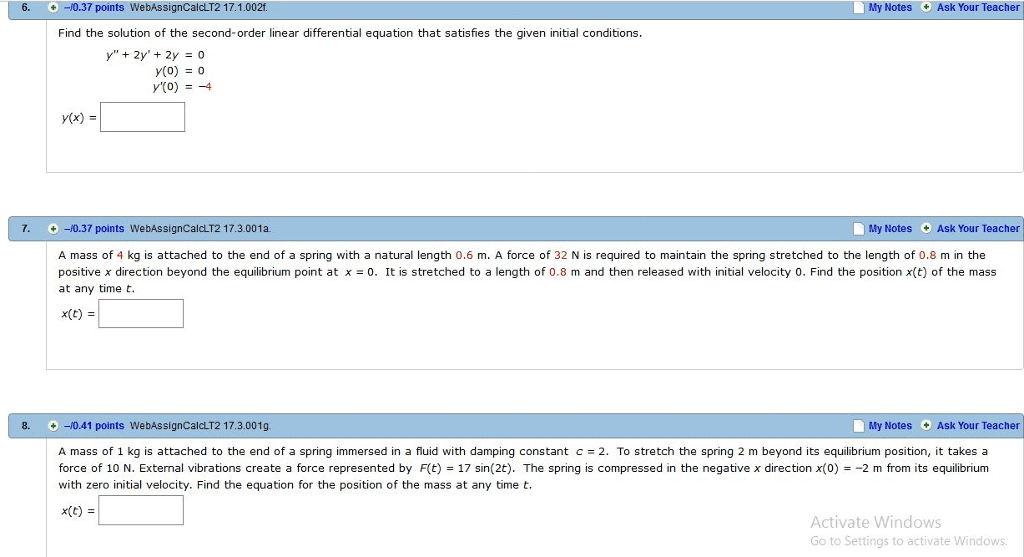
On the front of your bluebook write: (1) your name, (2) your student id number, (3) recitation section, (4) your instructor"s name, and (5) a grading table. Books, class notes, cell phones, and calculators are not permitted. 6y = 0, y(0) = 2, y (0) = 5 y + 2y + y = 0, y(0) = 0, y (0) = 1. 2 (30 points) consider the harmonic oscillator system: Assume that the mass of the block is m = 2, the spring constant k = 4, and that the equilibrium position of the block is x = 0. Both the damping constant b and the external force f (t) can vary. Write down the differential equation and nd the solution x(t) using the supplied initial conditions. Describe the motion of the block. (c) (14 points) suppose no damping is present (b = 0). An external force f (t) = cos(t) is applied to the block.