MA 141 Study Guide - Final Guide: Hyperbola, 32X, Ellipse
Document Summary
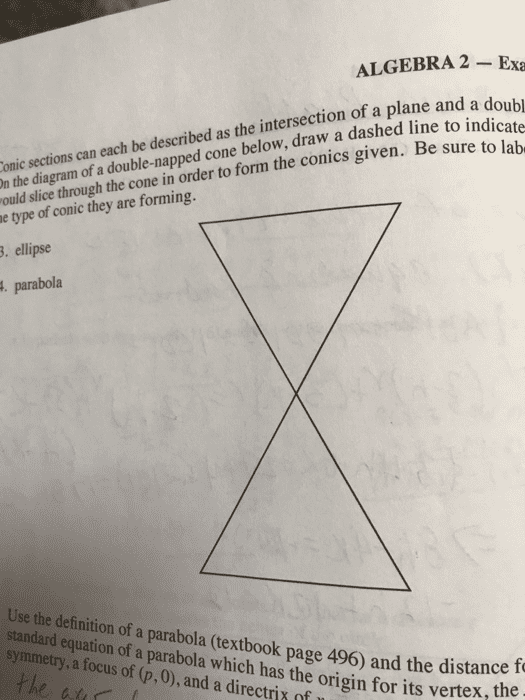
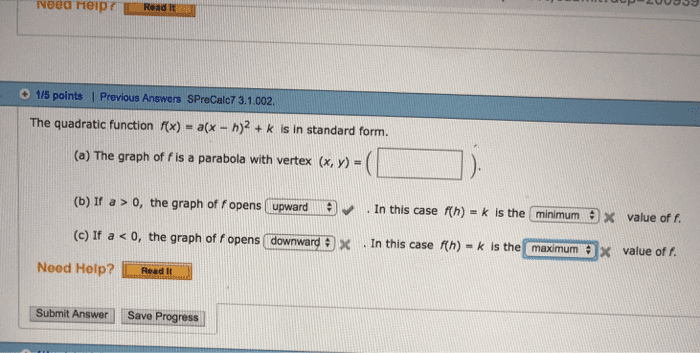
Distance formula: (derived from pythagorean theorem) given two points p = (x1, y1) and q = (x2, y2) in r2, the distance between them is d(p, q) =p(x1 x2)2 + (y1 y2)2. Def: a parabola is the set of points in the xy-plane that are equidistant from a xed point, the focus, and a xed line, the directrix. The vertex is the point of the parabola that minimizes the distance to the focus and directrix. The standard equation of the vertical parabola is. In this case, the focus is (cid:18)h, k + 4a(cid:19) and the directrix is y = k . If a > 0, the parabola opens upward and the vertex is the lowest point of the graph. If a < 0, the parabola opens downward and the vertex is the highest point of the graph. Similarly, we can have a parabola opening left or right. , k(cid:19) and the directrix is x = h .