MATH 4389 Study Guide - Final Guide: Diagonal Matrix, Invertible Matrix, Diagonalizable Matrix

• School: University of Houston
• Department: Mathematics
• Course: MATH 4389
• Professor: Almus

Document Summary

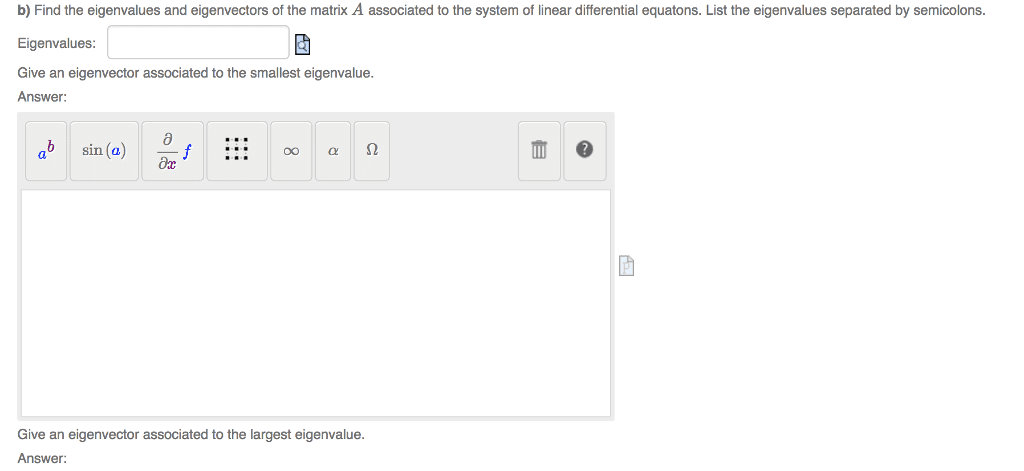
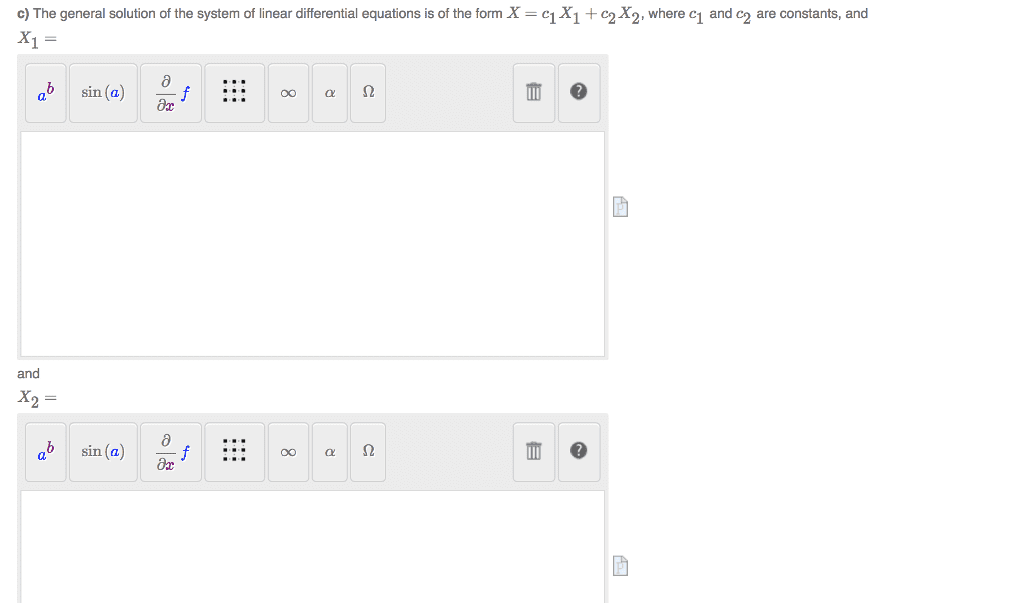
Definition: an eigenvector of an n n matrix a is a nonzero vector x such that. A scalar is an eigenvalue of a if there exists a nontrivial solution x of. ; such an x is called an eigenvector corresponding to . x ==== Show that 7 is an eigenvalue of a. Notice that ax x =(cid:1) (cid:1) for (cid:1) x. That is, x (cid:1) is an eigenvector corresponding to if and only if (cid:1) x nul a. I (cid:1) is an eigenvector corresponding to , Definition: if x is called the eigenspace for . Key fact: is an eigenvalue of a if and only if det( The characteristic polynomial of a is an nth degree polynomial in : p. Definition: algebraic multiplicity of an eigenvalue is the degree of the corresponding factor in the characteristic polynomial. Geometric multiplicity of an eigenvalue is the dimension of the corresponding eigenspace.