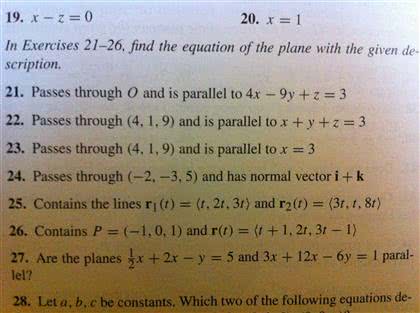
Please complete number 22 and explain step by step, thankyou.
X - z = 0 x = 1 In Exercises 21 - 26, find the equation of the plane with the given description. Passes through o and is parallel to 4x - 9y + z = 3 Passes through (4, 1, 9) and is parallel to x + y + z= 3 Passes through (4, 1, 9) and is parallel to x = 3 Passes through (-2, -3, 5) and has normal vector i + k Contains the lines r1(t) = and r2(t) = Contains P = (-1, 0, 1) and r(t) = Are the planes 1/2 x + 2x - y = 5 and 3x + 12x - 6y = 1 parallel? Let a, b, c be constants. Which two of the following equation de-
Show transcribed image text X - z = 0 x = 1 In Exercises 21 - 26, find the equation of the plane with the given description. Passes through o and is parallel to 4x - 9y + z = 3 Passes through (4, 1, 9) and is parallel to x + y + z= 3 Passes through (4, 1, 9) and is parallel to x = 3 Passes through (-2, -3, 5) and has normal vector i + k Contains the lines r1(t) = and r2(t) = Contains P = (-1, 0, 1) and r(t) = Are the planes 1/2 x + 2x - y = 5 and 3x + 12x - 6y = 1 parallel? Let a, b, c be constants. Which two of the following equation de-
