PHYS 106 Chapter Notes -Circular Motion, Angular Velocity, Angular Acceleration

79 views4 pages

azurekangaroo166

22 Nov 2012

School

Department

Course

Professor

For unlimited access to Textbook Notes, a Class+ subscription is required.

Document Summary

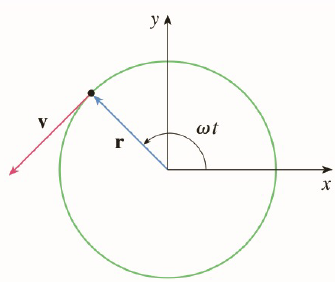
Motion at a constant speed around a circle. In other words, the velocity vector is always equal in magnitude, and always tangent to the circle. Period (t): the time it takes for an object to make one revolution, in seconds. We can describe the position of a particle in circular motion by the radius of the circle and the angle it makes counterclockwise from the x-axis. Relationship between arc length, angle, and radius: s= r where r is in radians. Use this to convert between degrees and radians. The change in a particle"s position in circular motion can be measured by finding the change in its angle, The average change in a particle"s angular displacement over time, is / t. Taking the limit as t-> 0 gives the: This is the rate at which a particle"s angular position is changing as it moves around the circle.

Related Questions

A particle P moves with constant angular speed ω around a circle whose center is at the origin and whose radius is R. The particle is said to be in uniform circular motion. Assume that the motion is counterclockwise and that the particle is at the point (R,0) when t=0. The position vector at time t≥0 is r(t)=Rcosωt i + Rsinωt j.

(a) Find the velocity vector v and show that v⋅r=0. Conclude that v is tangent to the circle and points in the direction of the motion.

(b) Show that the speed |v| of the particle is the constant ωR. The period T of the particle is the time required for one complete revolution. Conclude that

T=2πR/|v|=2π/ω

rosebeaver397

A particle P moves with constant angular speed ω around a circle whose center is at the origin and whose radius is R.The particle is said to be in a uniform circular motion. Assume that the motion is counterclockwise and that the particle is at the point (R, 0) when t = 0.The position vector at time t ≥ 0 is r(t) = R cos ωt i + R sin ωt j.

(a) Find the velocity vector v and show that v · r = 0. Conclude that v is tangential to the circle and points in the direction of the motion.

(b) Show that the speed of the particle is constant ωR. The period T of the particle is the time required for one complete revolution. Conclude T = 2π/ω.

goldpug777

You are given a circular conducting wire loop with one
end cut out and connected to a resistor, R, as shown in
the figure to the right. A metal rod of length l is set at an
initial angle ?0 from the resistor, and then rotates
clockwise about the center of the wire loop with angular
frequency through a uniform magnetic field B
directed into the page. The metal rod stays in contact
with the wire loop at all points of its motion. Unless
otherwise requested, all answers should be in simplified
algebraic form using the above given variables.

(a) Given that the initial angle ?0 is in radians, what is theinitial area of the closed circuit âwedgeâdefined by ?0? (2pts.)
(b) What is the magnetic flux through this initial âwedgeâ areadefined by ?0? (2 pts.)
Starting at time t=0 at position ?0, the rod is rotated clockwisewith angular velocity as shown in
the figure. Given this configuration, answer questions (c)-(g)below:
(c) What is the direction of the induced magnetic field inside theâwedgeâ? (2 pts)
(d) What is the direction of the induced current around the closedcircuit? (2 pts)
(e) What is the magnitude of the induced emf, E in the circuit? (4pts)
(f) What is the magnitude of the induced current in the circuit? (4pts)
(g) What is the power used by the resistor? (4 pts)
(h) The metal rod is now rotated in the opposite direction, i.e. inthe counter-clockwise direction. Given this information, completethe chart below as to what quantities you just calculated change,and what ones do not change. You do not have to show work, justgive the result. No partial credit will be given here. (5pts)

Direction of induced magnetic field inside the âwedgeâ.
Direction of the induced current around the closed circuit.
Magnitude of the induced emf, E in the circuit.
Magnitude of the induced current in the circuit.
Power used by the resistor.

The setup is now modified slightly so that the circular conductingwire loop no longer has a small
section removed as shown in both figures below. This modificationwould allow the metal rod to
continuously rotate on the circular wire loop as clearlyillustrated in the 3D side view. The metal rod
is rotated clockwise, as in the initial part of the problem.

(i) Given this information, complete the chart below. You do nothave to show work, just give the
result. No partial credit will be given here. (5 pts)

Direction of induced magnetic
field inside the âwedgeâ.
Direction of the induced current
around the closed circuit.
Magnitude of the induced emf, E in
the circuit.
Magnitude of the induced current
in the circuit.
Power used by the resistor.

PHYS 106 Chapter Notes -Circular Motion, Angular Velocity, Angular Acceleration

Document Summary

Get access

Related textbook solutions

Physics: Principles with Applications

Related Documents

PHYS 1080 Study Guide - Quiz Guide: Circular Motion, Angular Velocity, Angular Acceleration

PHYS 1003 Lecture Notes - Lecture 5: Circular Motion, Angular Frequency, Radian

PHY 1420 Midterm: Test 3 Notes

Related Questions