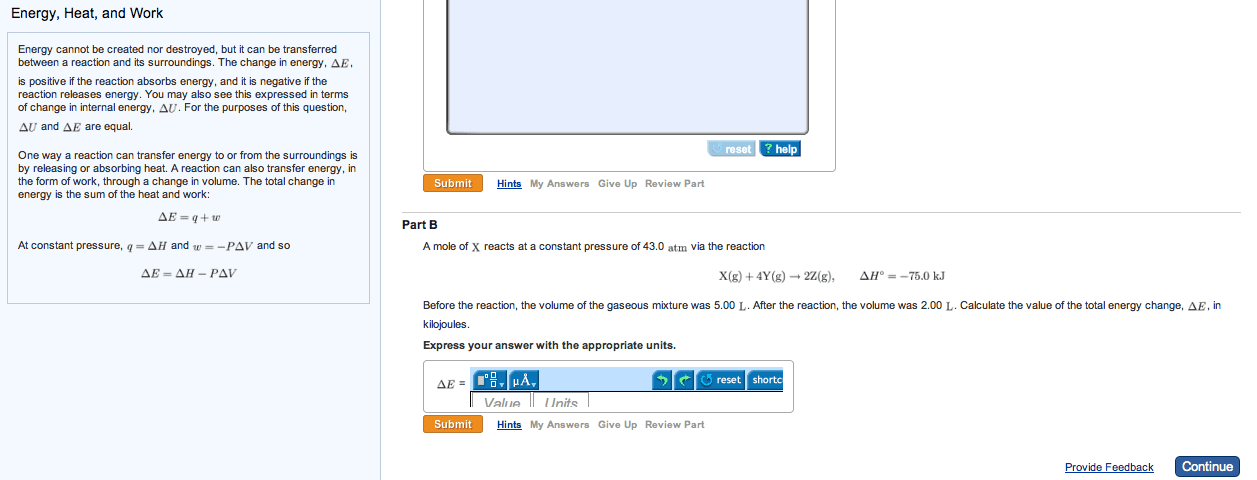
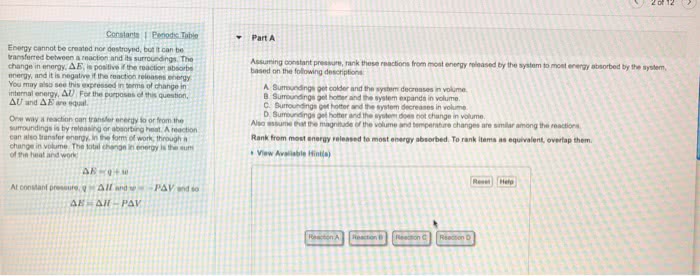
🏷️ LIMITED TIME OFFER: GET 20% OFF GRADE+ YEARLY SUBSCRIPTION →

HomeTextbook Notes300,000CA170,000

CHMB20H3 Chapter 2: CHMB20 Chapter 2

134 views6 pages

27 Sep 2011

School

Department

Course

Professor

Jamie Donaldson

For unlimited access to Textbook Notes, a Class+ subscription is required.

Document Summary

Thermodynamics: the study of the transformations of energy. System: the part of the world in which we have a special interest. Isolated system: a closed system that has neither mechanical nor thermal contact with its surroundings. system and its surroundings: work: done to achieve motion against an opposing force; the transfer of energy that makes use of organized motion. Endothermic and diathermic container results in energy flowing into the system as heat to restore the temperature to that of the surroundings. Exothermic and diathermic container results in a release of energy as heat into the surroundings. Endothermic and adiabatic container results in a lowering of temperature of the system. Exothermic and adiabatic results in a rise of temperature of the system. Thermal motion: disorderly motion of molecules in the surroundings (movement of heat). For monatomic gas (translation only), um(t) = um(0) + (3/2)rt, where. Um(-) is the molar internal energy at t = 0.

Related Documents

CHMB20H3 Lecture Notes - Calorie, Isolated System, Potential Energy

amethystreindeer873

CHMB20H3 Chapter 3: CHMB20 Chapter 3

CHM135H1 Final: Thermochemistry Review

Related Questions

Energy cannot be created nor destroyed, but it can be transferred between a reaction and its surroundings. The change in energy, Delta E, is positive if the reaction absorbs energy, and it is negative if the reaction releases energy. You may also see this expressed in terms of change in internal energy, Delta U. For the purposes of this question, Delta U and Delta E are equal. One way a reaction can transfer energy to or from the surroundings is by releasing or absorbing heat. A reaction can also transfer energy, in the form of work, through a change in volume. The total change in energy is the sum of the heat and work: Delta E = q + w At constant pressure, q = Delta H and w = -P Delta V and so Delta E = Delta H - P Delta V Assuming constant pressure, rank these reactions from most energy released by the system to most energy absorbed by the system, based on the following descriptions: Surroundings get colder and the system decreases in volume. Surroundings get hotter and the system expands in volume. Surroundings get hotter and the system decreases in volume. Surroundings get hotter and the system does not change in volume. Also assume that the magnitude of the volume and temperature changes are similar among the reactions. Rank from most energy released to most energy absorbed. To rank items as equivalent, overlap them. Energy cannot be created nor destroyed, but it can be transferred between a reaction and its surroundings. The change in energy, Delta E, is positive if the reaction absorbs energy, and it is negative if the reaction releases energy. You may also see this expressed in terms of change in internal energy, Delta U. For the purposes of this question, Delta U and Delta E are equal. One way a reaction can transfer energy to or from the surroundings is by releasing or absorbing heat. A reaction can also transfer energy, in the form of work, through a change in volume. The total change in energy is the sum of the heat and work: Delta E = q + w At constant pressure, q = Delta H and w = -P Delta V and so Delta E = Delta H - P Delta V A mole of X reacts at a constant pressure of 43.0 atm via the reaction X(g) + 4Y(g) - 2Z(g), Delta H degree = -75.0 kJ Before the reaction, the volume of the gaseous mixture was 5.00 L. After the reaction, the volume was 2.00 L Calculate the value of the total energy change. AE, in kilojoules. Express your answer with the appropriate units.