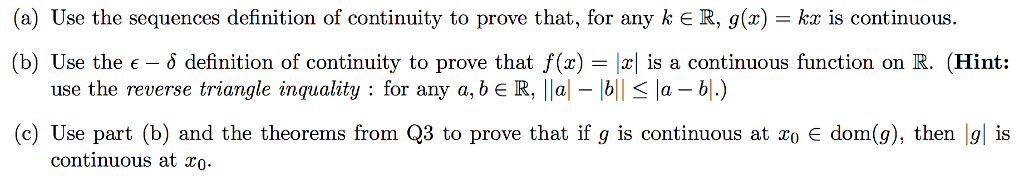MATH114 Lecture Notes - Lecture 9: General Idea, Asymptote

• School: University of Alberta
• Department: Mathematics
• Course: MATH114
• Professor: Alsaody,Seidon

Document Summary

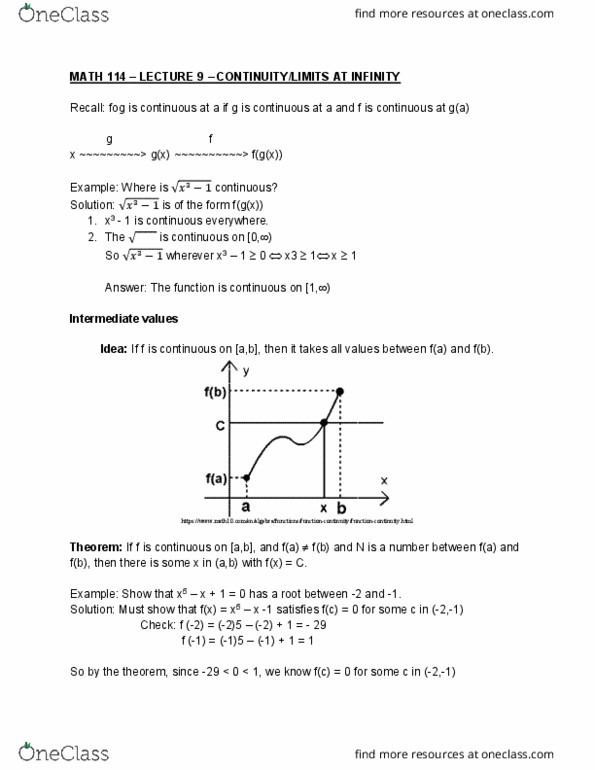
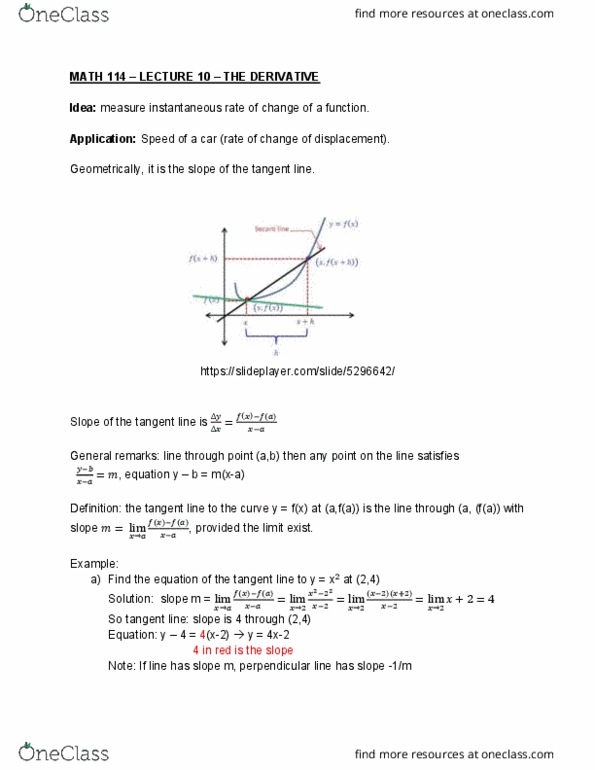
Math 114 lecture 9 continuity/limits at infinity. Recall: fog is continuous at a if g is continuous at a and f is continuous at g(a) g f x ~~~~~~~~~> g(x) ~~~~~~~~~~> f(g(x): x3 - 1 is continuous everywhere. Solution: (cid:1876)(cid:2871) (cid:883) is of the form f(g(x): the is continuous on [0, ) So (cid:1876)(cid:2871) (cid:883) wherever x3 1 0 x3 1 x 1. Idea: if f is continuous on [a,b], then it takes all values between f(a) and f(b). https://www. math10. com/en/algebra/functions/function-continuity/function-continuity. html. Theorem: if f is continuous on [a,b], and f(a) f(b) and n is a number between f(a) and f(b), then there is some x in (a,b) with f(x) = c. Example: show that x5 x + 1 = 0 has a root between -2 and -1. Solution: must show that f(x) = x5 x -1 satisfies f(c) = 0 for some c in (-2,-1)