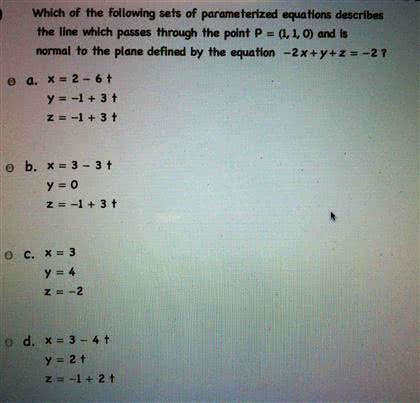
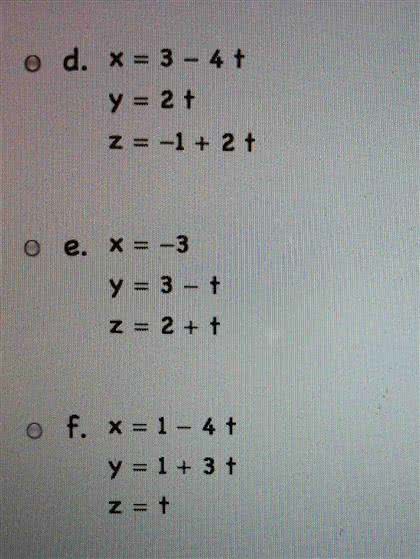MATH 263 Midterm: MATH 263 2006 Winter Test 1
Document Summary
Suppose that the electrical potential v in space is given by the function. What is the rate of change of the electrical potential when the particle passes through the point h1, 1, 0i. Find the absolute minimum of the function f (x, y) = 4 + 2xy x y on the triangle bounded by the lines x = 0, y = 0 and x + y = 2. For what value of a is the vector eld. For this value of a nd a function f (x, y, z) such that f = f . Let e be the solid (in the rst octant) bounded by the coordinate planes and two parabolic cylinders z = 1 x2 and z = 1 y2. Make a sketch of e and nd its volume. Make a sketch of the region of integration. F(x, y, z) = hxez 3y, yez 2. + 2x, x2y2z2i (we are using the notation f for curl (f). )