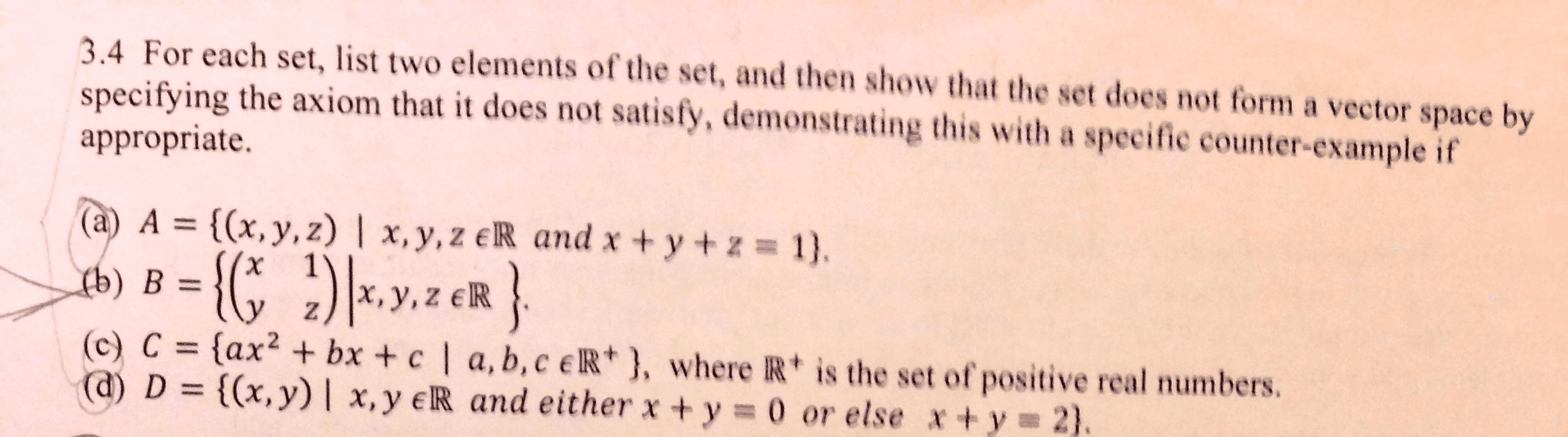MATH 104 Lecture Notes - Demand Curve, Constant Function, Exponential Growth

73
MATH 104 Full Course Notes
Verified Note
73 documents
Document Summary
Calculus is the study of functions on real numbers. De nition 1. a function y = f (x) is a rule that applies to some set of real numbers d, and for each x in the set d, it assigns it a unique real number y. The set d is called the domain of f . If f (x) = x2, then we can take the domain d to be the set of all real numbers. If f (x) = 1/x, then f is de ned at every point x (cid:54)= 0. If f (x) = x, then f is de ned at every x 0. We can de ne a function by its graph, and much of calculus comes from draw- ing connections between the algebraic side (i. e. an equation) and the graphical side (i. e. the graph of a function). For example, here is the graph of f (x) = x2: