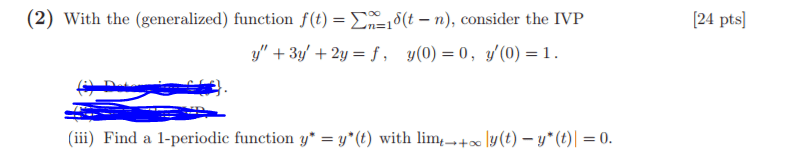MATH 1272 Lecture Notes - Lecture 1: Arc Length
Document Summary
To find a double point or a point of self-intersection on a parametric curve, we want to find two times t sub 1, t sub 2 so that (x(t sub 1),y(t sub 1))=(x(t sub 2),y(t sub 2)). 2nd equation zeros of t sub 1=0,2,-2,1,-1 t. Solve[{x[t sub 1]==x[t sub 2],y[t sub 1]==y[t sub 2]},{t sub 1, t sub 2}] On small scales, we can think of y as being a function of x y=f(x) slope of tangent line is just dy/dx. But! everything is in terms of t! y(t)=f(x(t)) Evaluate at time t, get slope of tangent line at (x(t),y(t)) Find equations of tangent lines to this curve at (-3,0) At (-3,0), the two tangent lines are y-0=6(x+3) y-0=-6(x+3) At t=0, there is an unusual inflection point, where t changes direction. Find the area between a parametric curve and the x-axis. Curve given by x=x(t), y=y(t), e t f x=x(t) dx=x"(t) f=y(t) x(f)=c x(e)=d.