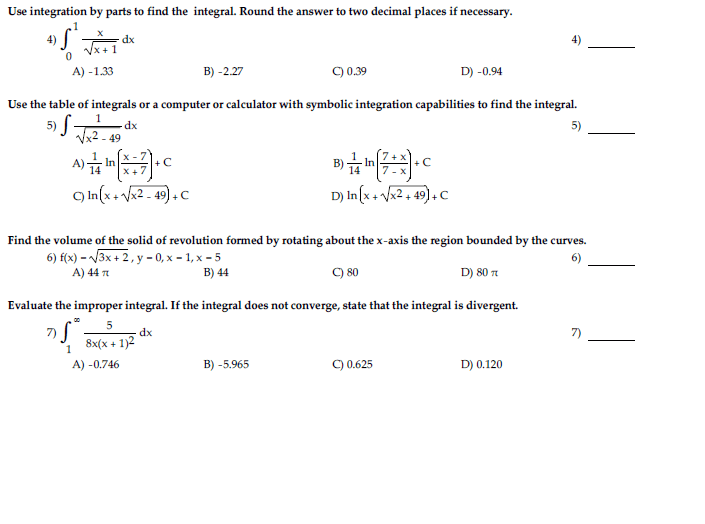MATH 1272 Lecture 1: 7.8- Improper Integrals
Document Summary
We can estimate this by looking at. Provided the limit exists (is a real number) If both exist (all real numbers valued) for some a in all real numbers, If the limits in (a) or (b) exist (real #), we say the improper converges or is convergent. If limits are or dne otherwise, we say the diverges or is divergent. Since sin x does not rest on a number when gong to , we cannot consider our bumps cancel out. By ftc since tan is continuous on [0,t] We know that sec(t) (cid:736) + as t(cid:736) /2 from the left. If f is continuous on [a,b), discontinuous at b, then. If f is continuous on (a,b], discontinuous at a, then. If f is continuous on [a,c)u(c,b] and discontinuous at c, Would suggest the is zero, since this region we are considering is symmetric and the areas should cancel out.