MATH237 Quiz: MATH237 : MATH237 : Asst09

• School: University of Waterloo
• Department: Mathematics
• Course: MATH237
• Professor: Changbao Wu

Document Summary

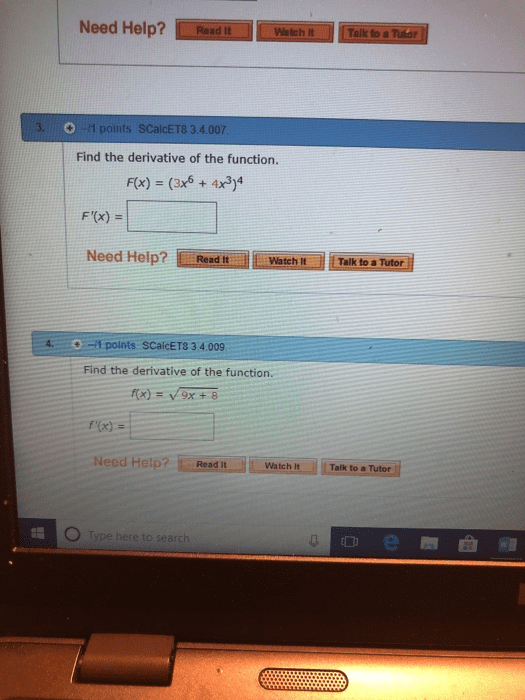
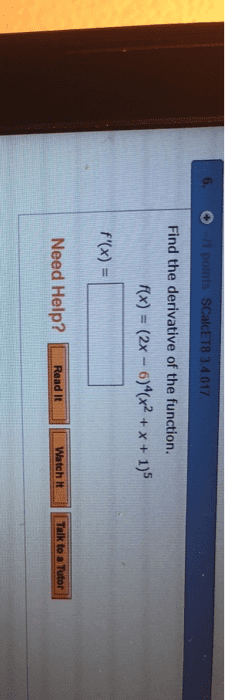
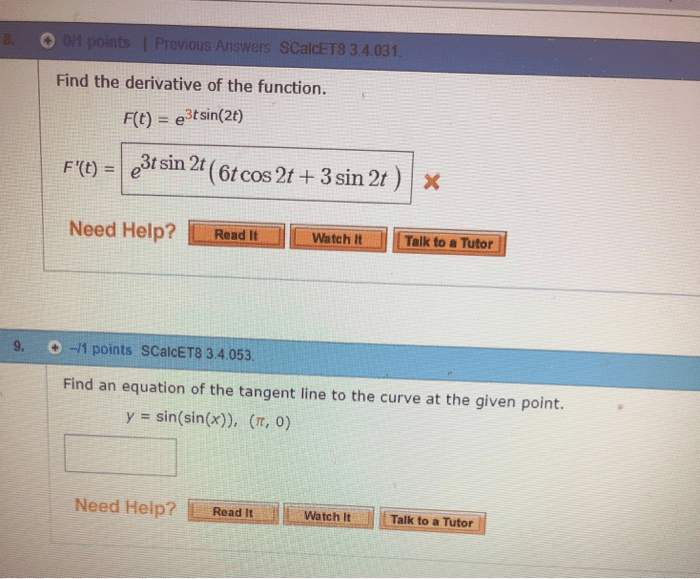
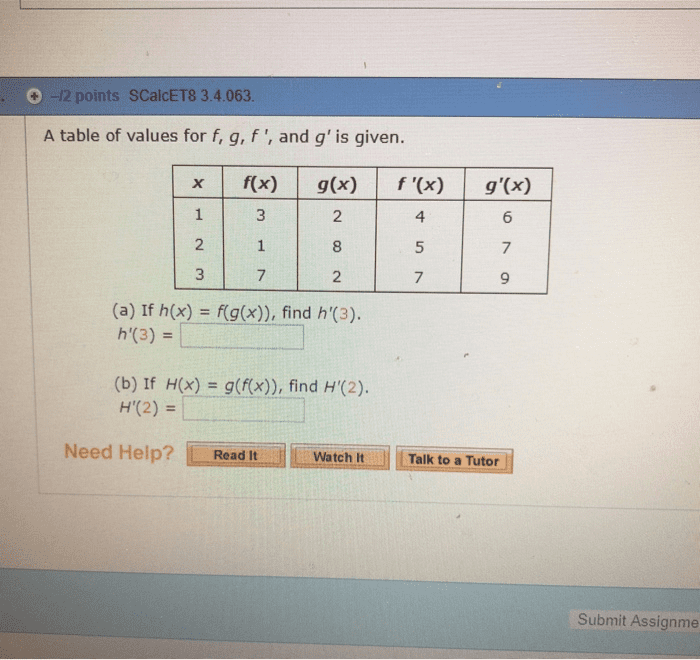
Submit your work at the usual time and place on wednesay, july 13th. Late assignments or those put into the wrong drop slot will not be marked and will receive a grade of zero: consider the maps f and g de ned by. F (u, v) = (v + u2, u), State the chain rule in matrix form, and use it to calculate the derivative d(f g)(0, 1) of the composite map: calculate the jacobian. (x, y) for the following map t . Find all points at which the jacobian is zero. Use the inverse map theorem to prove that t 1 exists in a neighbourhood of the indicated point: (u, v) = t (x, y) = (cos(x + y), sin(x y)); (cid:16) .