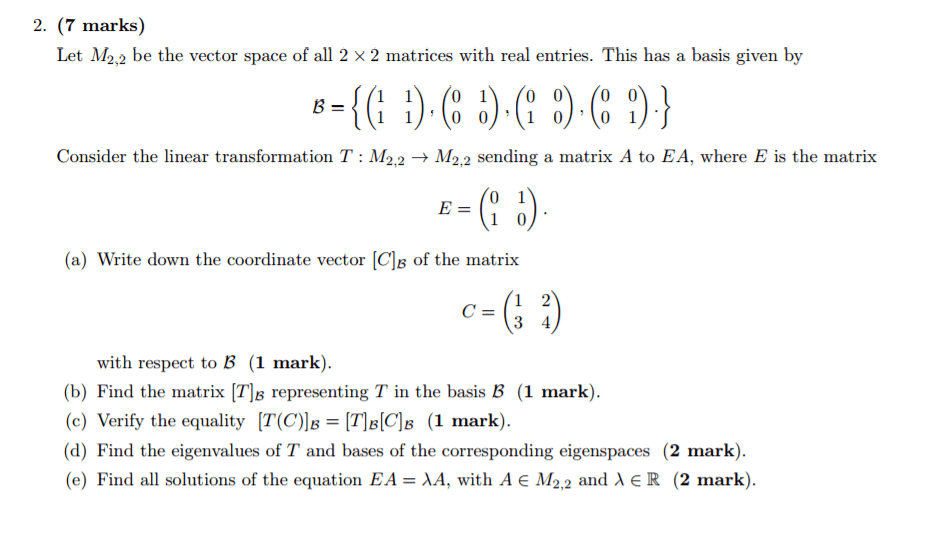MATH 271 Final: MATH 271 Amherst F17M271Final

• School: Amherst College
• Department: Mathematics and Statistics
• Course: MATH 271
• Professor: All

Document Summary

Final exam: true or false: (no justi cation necessary) (a) (b) If a and b are n n matrices such that ab is the zero matrix, then either. A is the zero matrix or b is the zero matrix. The set of vectors {(1, 0, 0), (1, 1, 0), (1, 1, 1)} is a basis for r3. (c) The set of polynomials of degree exactly 3 is a vector space. (d) (e) If an n n matrix a is diagonalizable, then a has n distinct eigenvalues. Every orthogonal set of nonzero vectors in rn can be extended to an orthogonal basis of rn. , and consider the map t : r3 r4. Determine if b im(t ): suppose t : m2 2 m2 2 is the linear transformation whose matrix representation with respect to the basis b = 1 0. Find a basis for ker (t ) and a basis for im(t ): let a = 2.