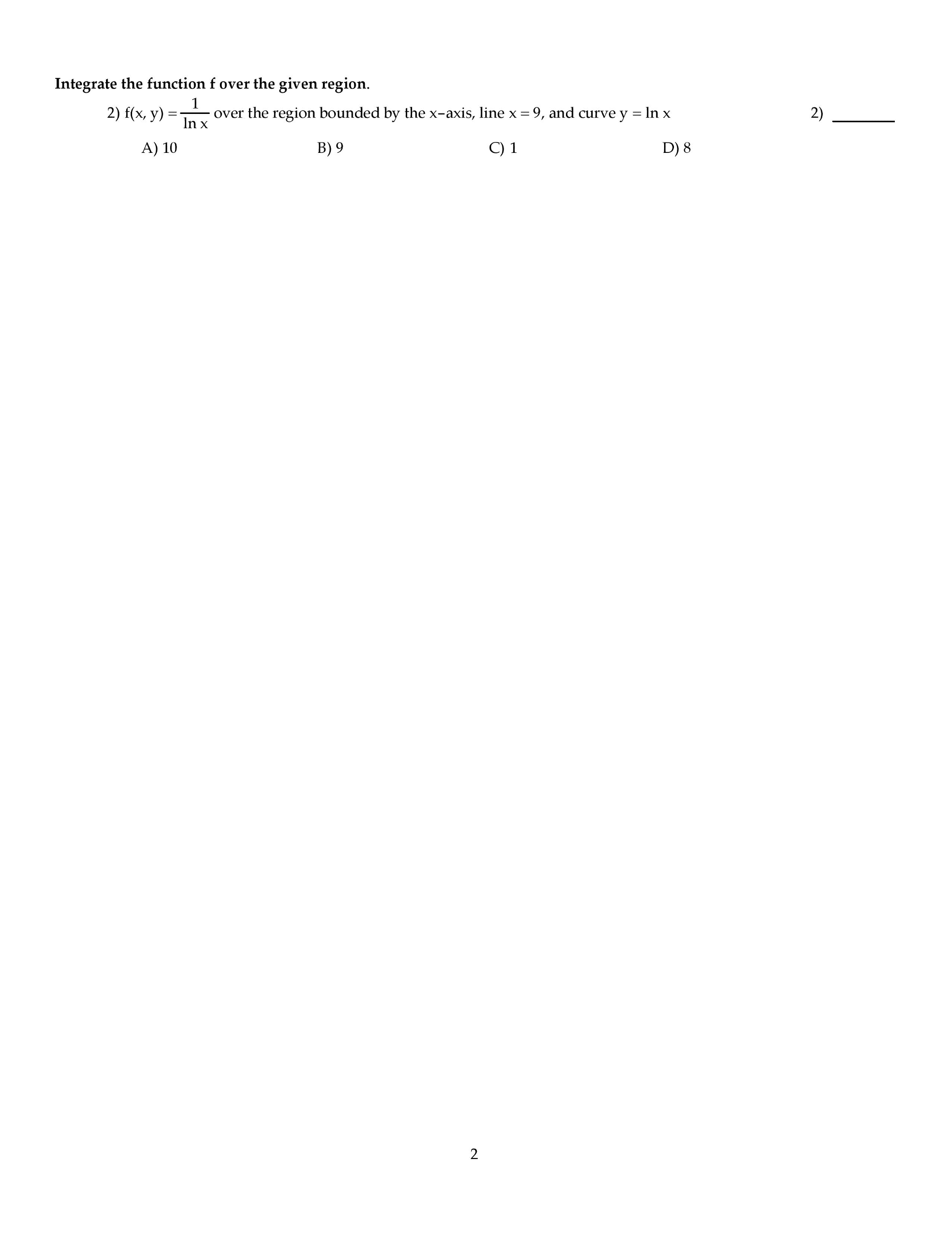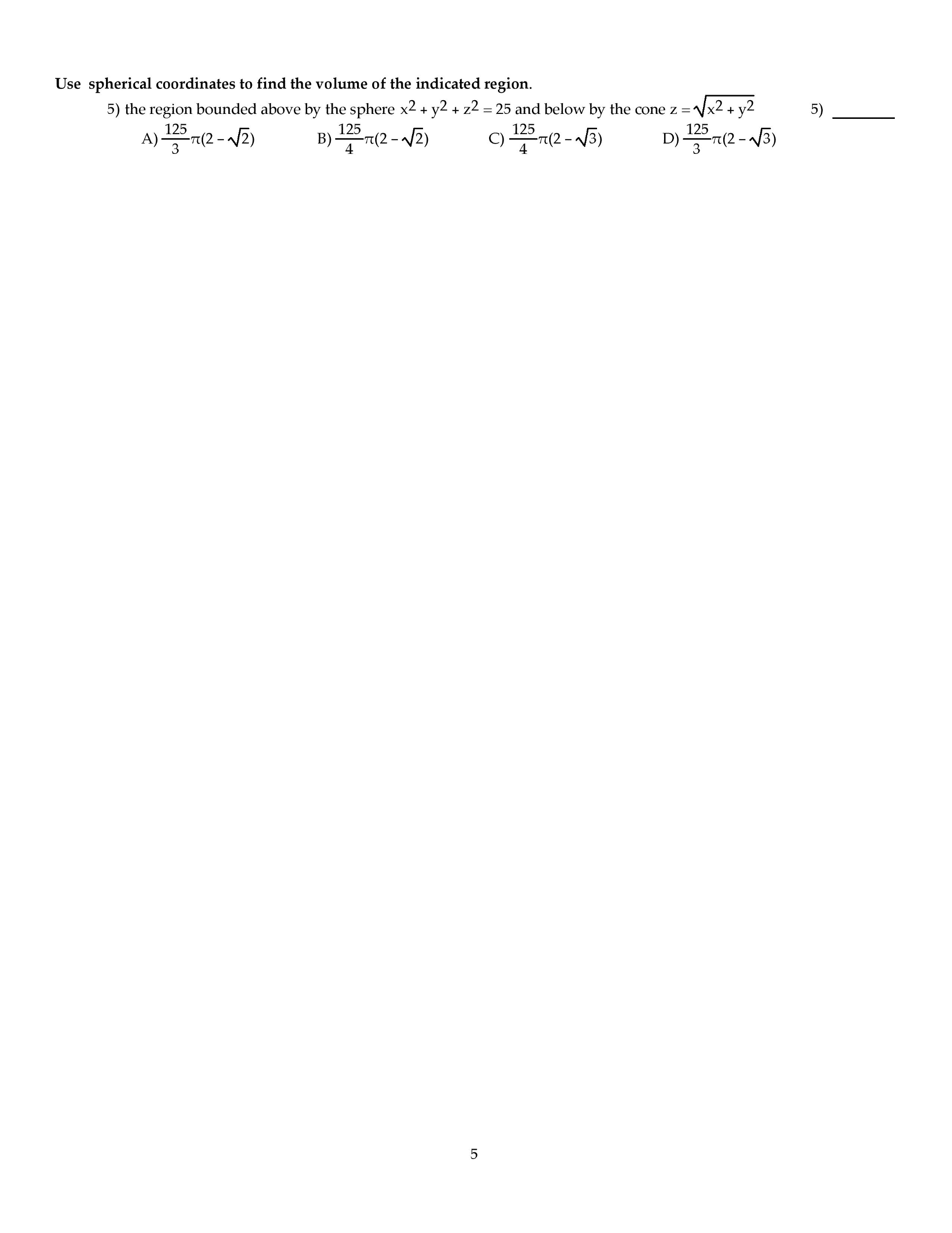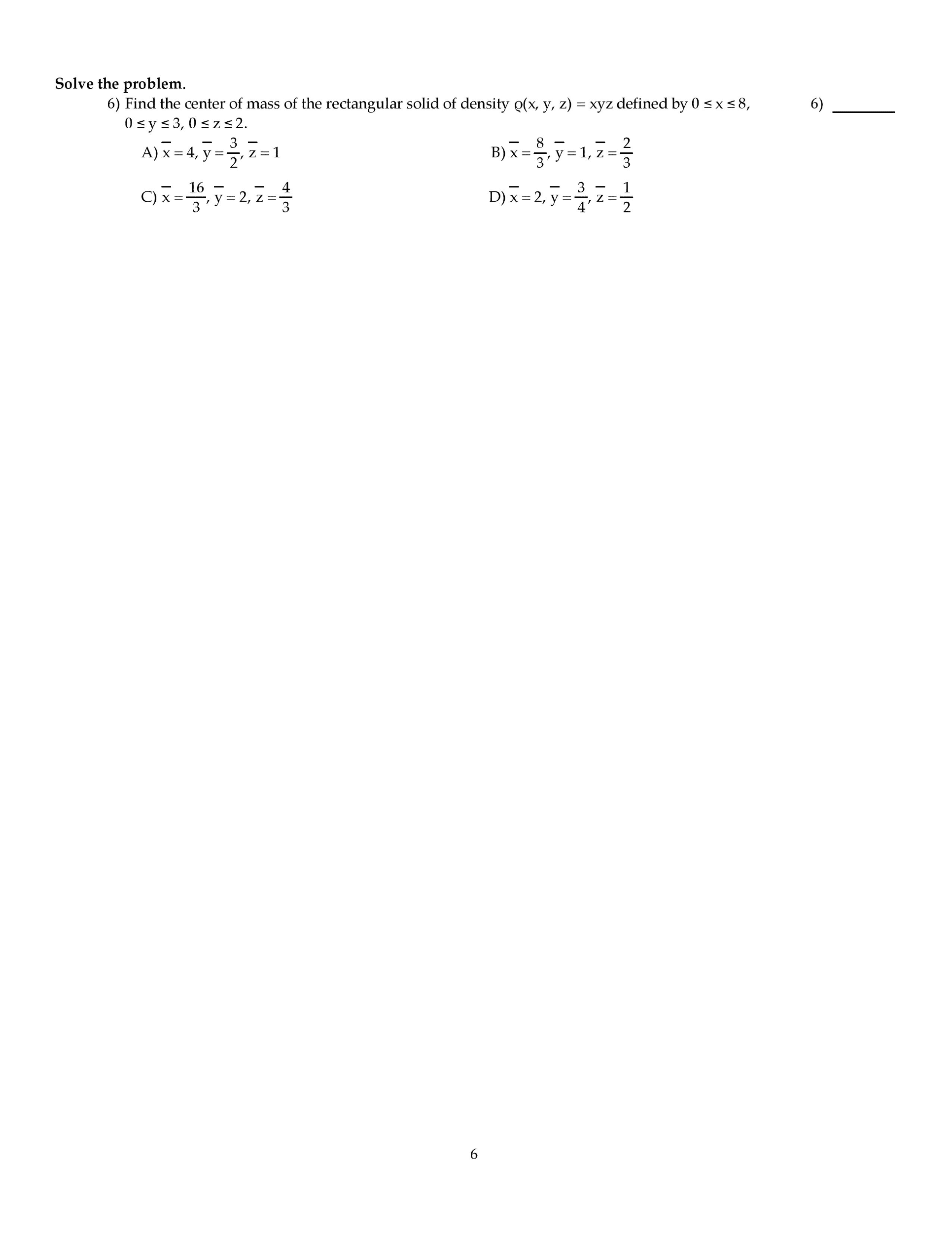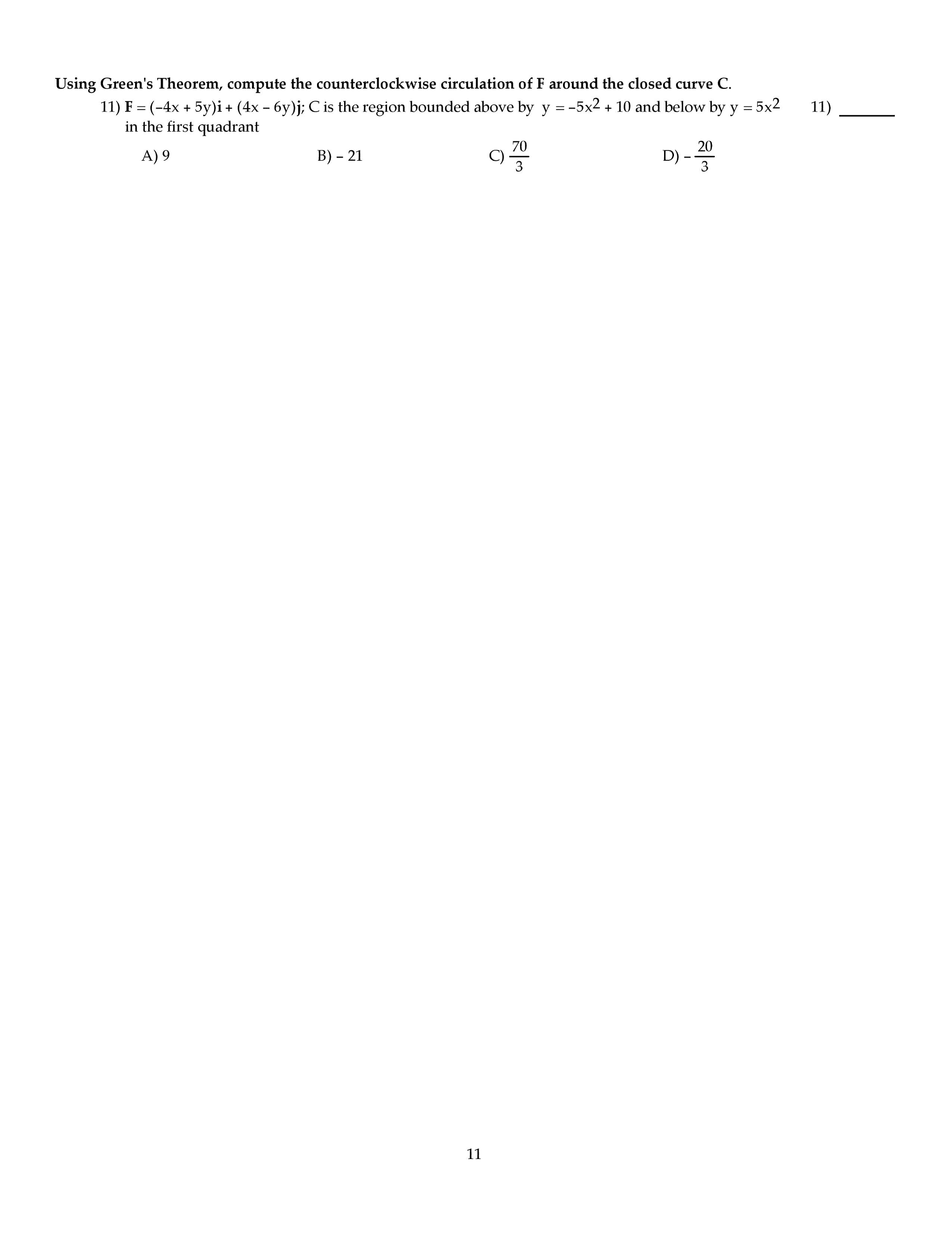HomeStudy Guides420,000US230,000

MATH-275 Final: MATH 275 Boise State Final takehome short

34 views1 pages

turquoisegnu128

15 Feb 2019

School

Boise State University

Department

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

Spring 2017: (10 points) an object moves counter clockwise along a circular path of radius 2, starting at the point p (2, 0) through the vector. Verify green"s theorem in this example by computing the work along this path in two di erent ways. (a) compute the line integral directly. Clearly state the param- eterization used, and show how to write the line integral using the parameterization. (b) using green"s theorem. Show all work to compute the integral by hand: (10 points) find the ux of the vector eld. F (x, y, z) = (cid:10)xyz, y2z, xz2(cid:11) through the surface s, which is the right side of the cylinder x2 + y2 = 4 with y 0 between the planes z = 0 and z = 5.

Related textbook solutions

Calculus

ISBN: 9781319050733

Single Variable Calculus: Early Transcendentals

4th Edition, 2018

ISBN: 9781337687805

CALCULUS:EARLY TRANSCENDENTALS

ISBN: 9781319050740

Related Documents

MATH-275 Final: MATH 275 Boise State Final prac

turquoisegnu128

MATH-275 Final: MATH 275 Boise State Final studyguide

turquoisegnu128

MATH 241 Midterm: MATH 241 UIUC Math241_Exam4_9AM_Fall10

turquoisegnu128

Related Questions

Solve all please.

INSTRUCTIONS: There are 15 problems on this exam, and each problem is worth 13 points, plus 5 points for writing down an approximate volume of the planet Earth in cubic miles at the bottomleft corner of page 3, for a total possible 200 points. For this exam, you are allowed to use one 8.5"X11" sheet of notes (both sides, in your own handwriting), pencil, eraser, ruler, scratch paper and calculator. Even though the questions are multiple-choice, you need to show enough work to justify your answer in order to receive full credit. After you have determined the correct solution to each problem, write the letter corresponding to your answer in the appropriate space on the right side of the page AND circle your answer. If your answer does not agree with any of the choices, after double-checking your work, choose option E) and prominently mark your answer (box, circle, underline, etc.). Time limit: Two hours. Attach (i.e. staple) any notecard and scratch paper to the rear of this exam paper. Good luck! MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. The northern third of Indiana is a rectangle measuring 96 miles by 132 miles. Thus, let D = [0, 96] times [0,132]. Assuming that the total annual snowfall (in inches), S(x,y), at (x,y) euro D is given by the function S(x,y) = 60e-0.001 (2x + y) with (x,y) euro D, find the average snowfall on D. 51.14 inches 52.06 inches 51.78 inches 52.44 inches Evaluate the work done between point 1 and point 2 for the conservative field F. Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C. Evaluate the surface integral of G over the surface S. S is the portion of the cone Find the flux of the vector field F across the surface S in the indicated direction. Using the Divergence Theorem, find the outward flux of F across the boundary of the region D. Integrate the function f over the given region. f(x,y) = 1/ln x over the region bounded by the x-axis, line x = 9, and curvey y = ln x Reverse the order of integration and then evaluate the integral Use a double integral in polar coordinates to find the area of the region specified in polar coordinates. the region inside both r = 7 sin Theta and r = 7 cos Theta Use spherical coordinates to find the volume of the indicated region. the region bounded above by the sphere x2 + y2 + z2 = 25 and below by the cone z = Find the center of mass of the rectangular solid of density (x,y,z) = xyz defined by 0 LE x LE 8, Use the given transformation to evaluate the integral. where R is the parallelogram bounded by the lines y = 8x + 8, y = 8x +9, y = -6x + 2, y = -6x +7 Evaluate the line integral along the curve C. Find the work done by F over the curve in the direction of increasing t.