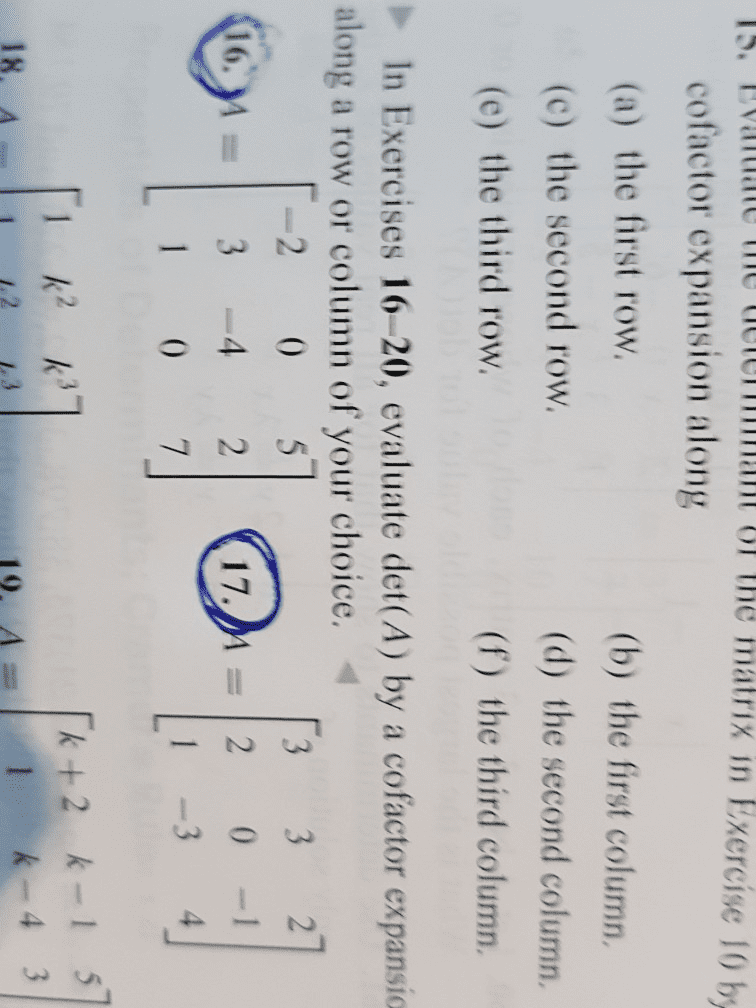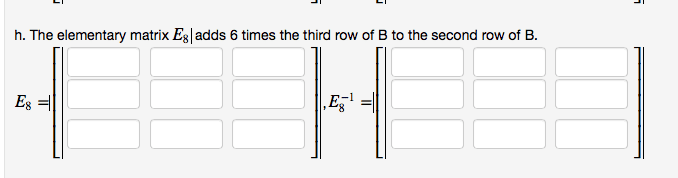21127 Study Guide - Quiz Guide: Pigeonhole Principle, Fair Coin, Lattice Path
16 Dec 2015
School
Department
Course
Professor
Document Summary
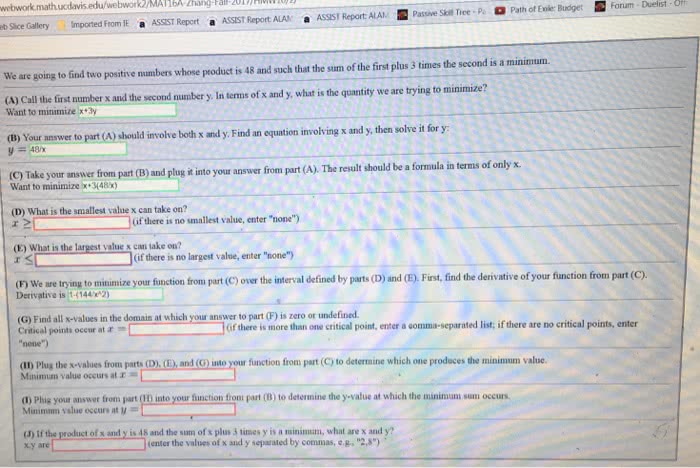
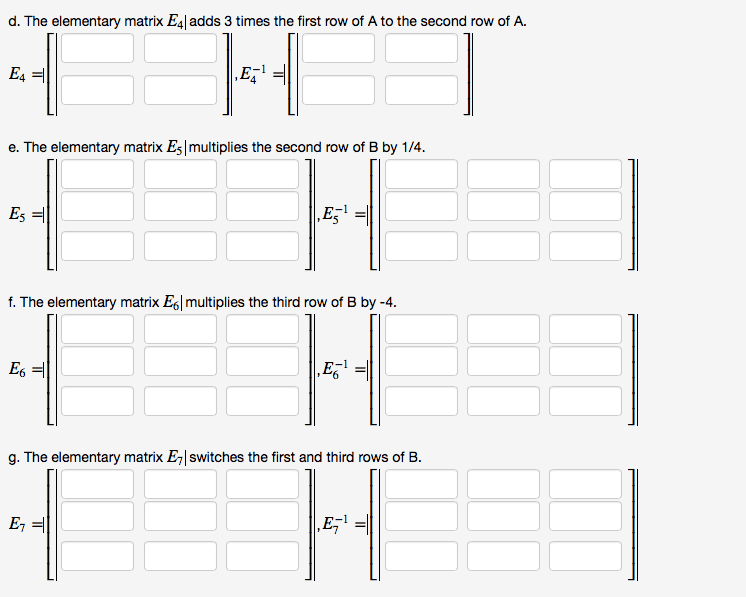
Pigeonhole principle (1) there are 5 professors in the math department. Every year, 2 are chosen to teach concepts. Prove this is optimal by exhibiting such a sequence of that length, as well as invoking the pigeonhole principle to show that any longer sequence necessarily uses a pairing more than once. (cid:1) = 10. Thus, we conjecture that, at best, we can go 10 years in a row without. For any 11 years in a row (or more), we are guaranteed to repeat a selection. First, we will show that we can go 10 years in a row without repeating a selection. Suppose the 5 professors are a, b, c, d, e. notice that the following sequence of 2-selections is of length 10 and does not repeat any 2-selection: {a, b},{a, c},{a, d},{a, e},{b, c},{b, d},{b, e},{c, d},{c, e},{d, e} Second, we will show that any 11 years in a row must repeat a selection.
