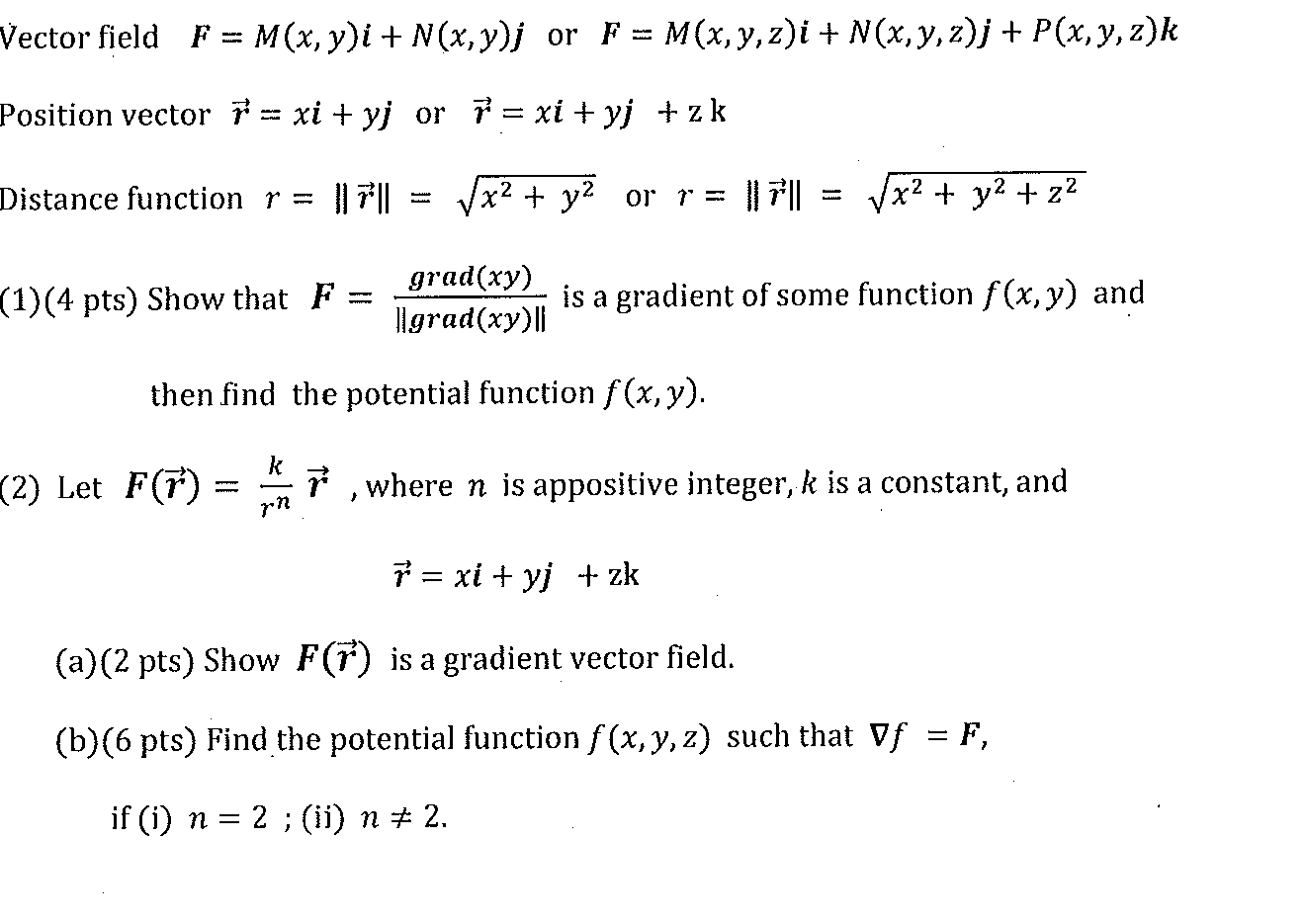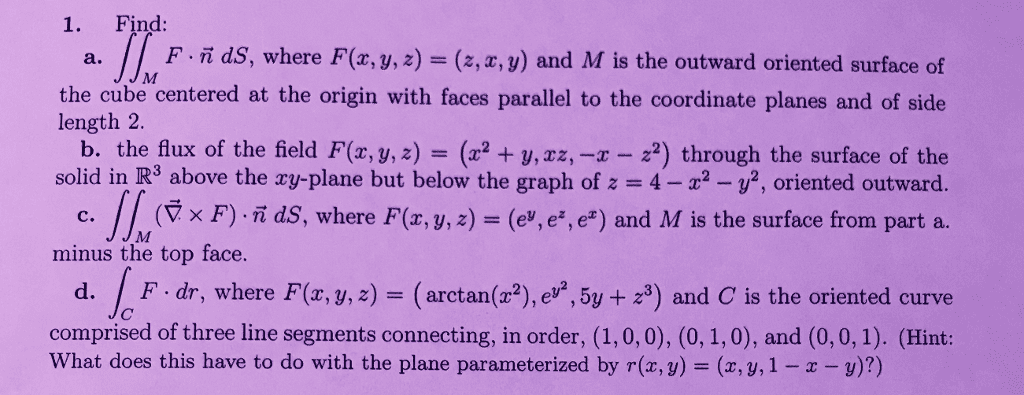MATH 2400 Quiz: Quiz2Solutions
Document Summary
June 13, 2012: let f be the function f (x, y) = c + mx + ny, where c, m, n are constants and n 6= 0. Show that all the contours of f are lines of slope m n. This is a line with slope m n . n x + r c: find a function f (x, y, z) whose level surface f = 1 is the graph of the function g(x, y) = arctan(x2 y2). Solution: the graph of the function g(x, y) = arctan(x2 y2) is the collection of points (x, y, z) such that z = arctan(x2 y2). Consider the function f (x, y, z) = arctan(x2 y2) z + 1. Suppose we consider the value of the function for non-zero points along the x-axis. In particular, any non-zero point on the x-axis is of the form (x, 0) where x 6= 0.