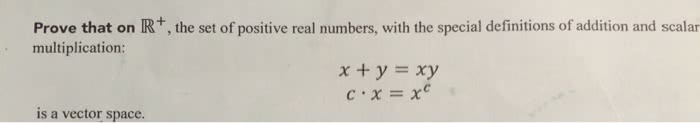MAD 4301 Midterm: MAS4301 F05 Test 2
Document Summary
October 12, 2005 (1) (15 points) complete the following de nitions. (a) let r be a ring, and a an element of r. we say that a is a unit . (b) let r be a ring. We say r has no zero divisors . (c) let r be a ring and a r {0}. If as = 1 for some s > 0, the order of a (d) let r be a ring. Proofs are not re- quired, nevertheless, be speci c and describe your examples carefully. Proof: (6) (10 points) if f is a eld, then f has no zero divisors. Proof: (7) (10 points) if m > 1 is composite, then z/m has at least one zero divisor. Proof: (8) (10 points) if m > 1 and z/m is a eld, then m is a prime number.