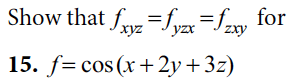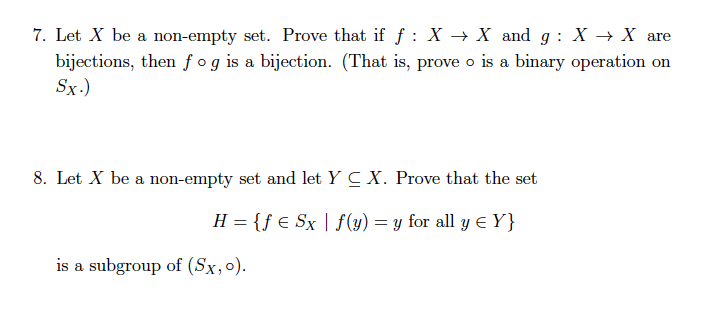MAD 4301 Midterm: MAS4301 F05 Test 4
Document Summary
If p f [x], we say p is a greatest common divisor of f and g . (f) let f be a eld, f and g polynomials in f [x]. We say f and g are associates . (g) let f be a eld, p a polynomial in f [x]. We say p is irreducible . (2) (5 pts. ) Give without proof the statement of bezout"s identity for the ring. F [x], where f is any eld. (3) (20 pts. ) State and prove euclid"s lemma for the ring z. (6) (15 pts. ) Prove using mathematical induction: for all n 0, 1 + x + x2 + + xn = xn+1 1 x 1. If g is a nite abelian group of order n, then for each a in g, an = e. proof: (8) (15 pts. ) Let f be a eld, p(x) and f (x) polynomials in f [x], and assume p(x) is irreducible.