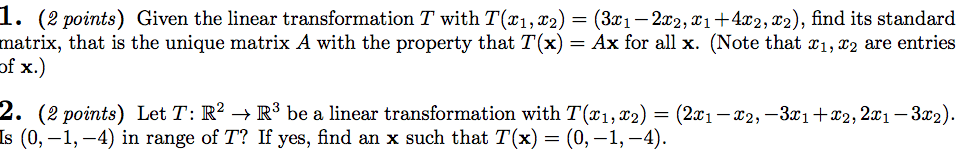MATH 551 Midterm: MATH 551 KSU Sample2Test2 f06

• School: Kansas State University
• Department: Mathematics
• Course: MATH 551
• Professor: All

Document Summary

Second sample of test 2 (chapters 3, 4, 5, and 6) Let t : r3 r3 be the linear transformation given by. T (x1, x2, x3) = x1 + x2 x3 x1 + x3. 0 (i) find a 3 3 matrix a such that t x = ax for every x = (x1, x2, x3) r3. (ii) find a basis for range(t ). What is rank(a)? (iii) let b = [0 0 0] . Find x and y such that the matrix q given by. Find the area of the parallelogram whose sides are the vectors u = [1, 3, 5] and v = [0, 2, 2] . Suppose that we have three square matrices a, b, and c such that a is invertible and ab2 = c t at . T (x1, x2) = x1 x2. (ii) yes - no. T (x1, x2, x3) = [x1 + x2 + 1, 3x1 x2] .