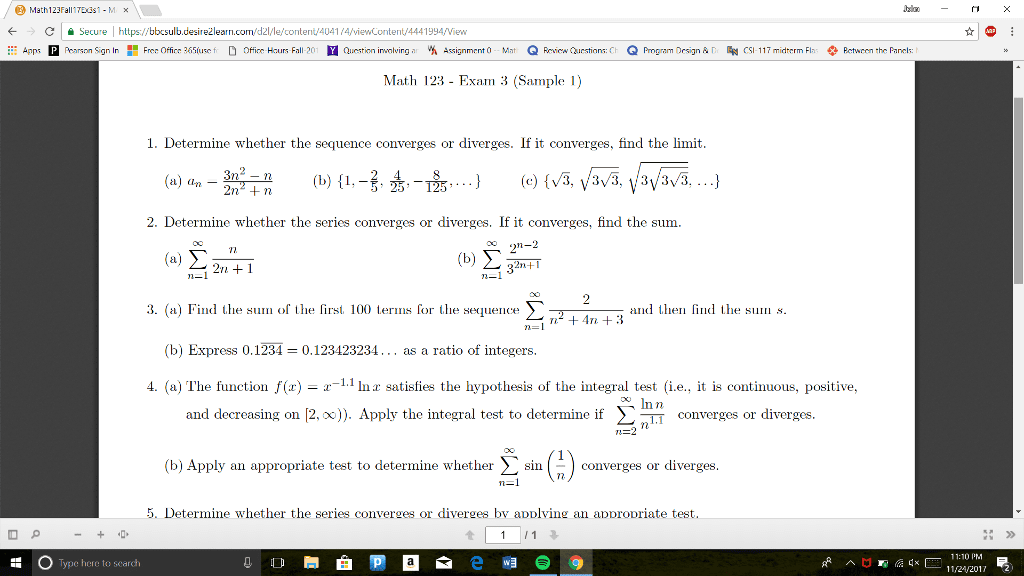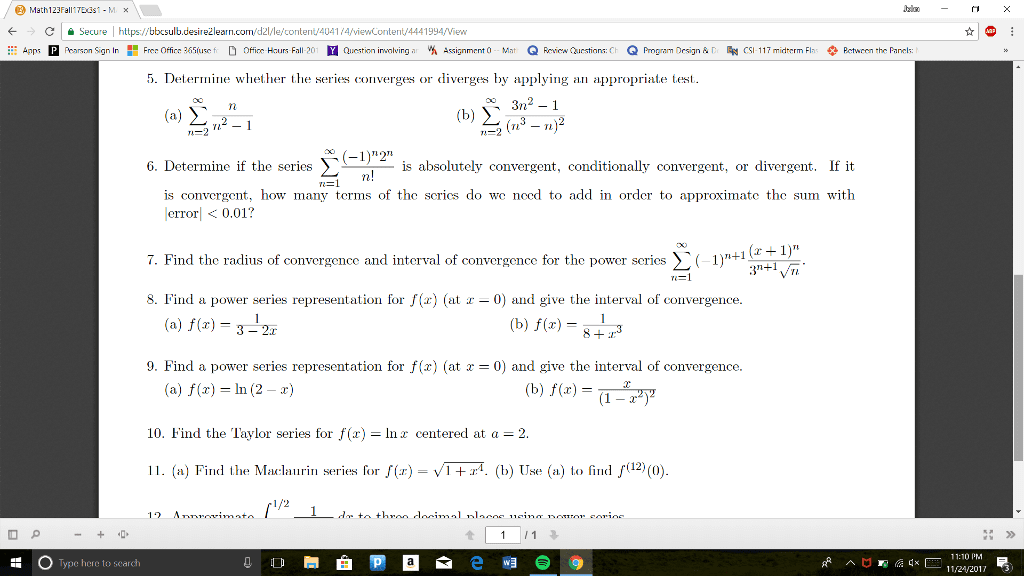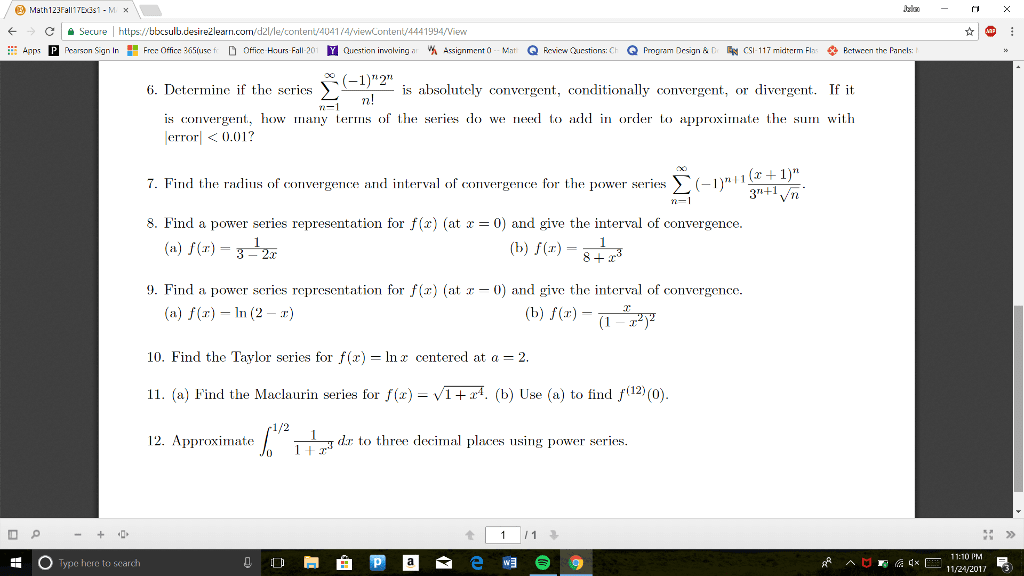MTH 151 Midterm: MTH 151 - Term Test 3
Document Summary
Given the graph, what is the distance travelled . In total? (from t = 0 to t = 5) So we know that the graph shows the relationship between velocity (miles per hour) and time (hours) Using the givens, between 1 and 4 pm is 3 hours, and the speed is constant at 40 mph. So d = (40)(3) = 120 miles. This is a fact that within a velocity time graph, the area under the curve is the distance travelled. Knowing this information, we can then solve for the distance by finding the area under the curve between t = 0 and t = 5. We can either break this into two triangles and a rectangle, or simply use the equation of area for a trapezoid. ( )(b1 + b2)(h) in which b1 is equal to base 1, b2 is base 2, and h is the height. So say we have the function y = x^2.