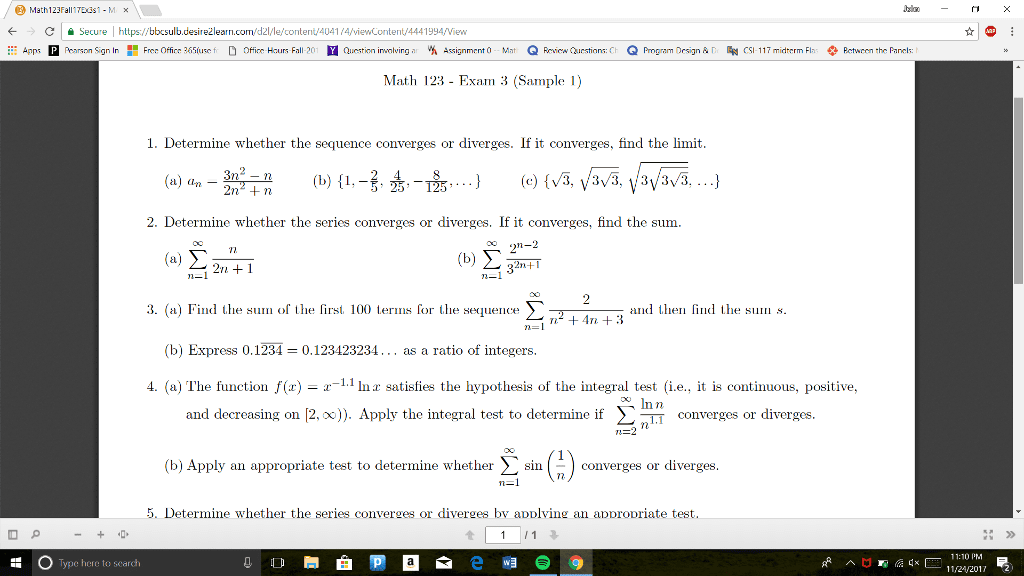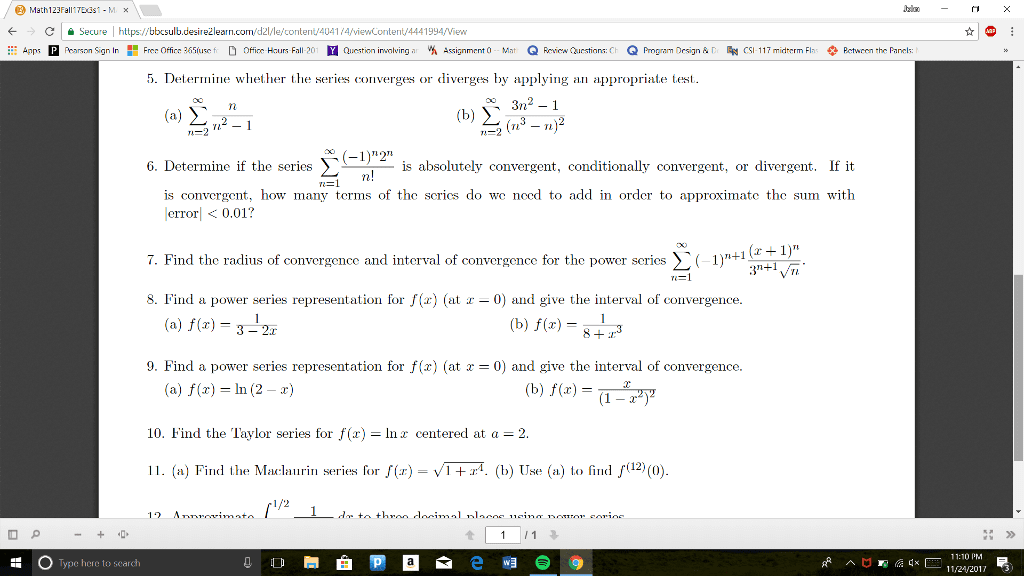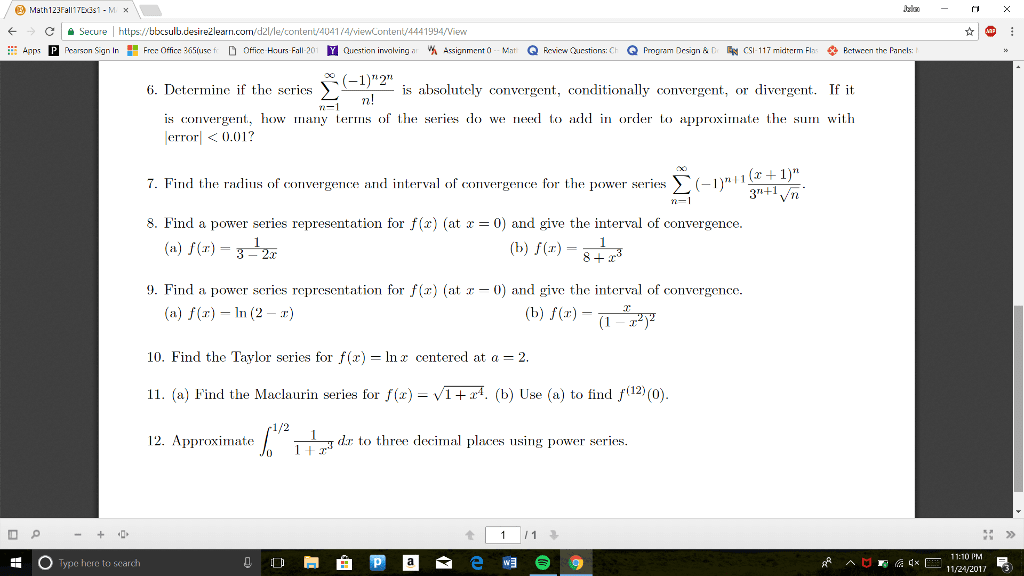HomeStudy Guides420,000US230,000

MTH 320 Midterm: Math 320 Exam 1 V2

30 views2 pages

turquoisegnu128

31 Jan 2019

School

Department

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

Summer 2015: (10 points) prove that for all n 2, > n. (hint: to show the base case (n = 2), you must show that 1 + 1/ 2 > 2. Recall that if a, b are positive, then a > b i a2 > b2. So try showing that a2 b2 > 0 for the appropriate choice of a and b. ) For the base case we follow the hint (twice). (cid:18)1 + since 2 > 1. N + 1: (10 points) use an -n argument to prove n + 1. Let > 0 and let n = 2/ + 10. = (cid:12)(cid:12)(cid:12)(cid:12) n2 + 2 5(cid:12)(cid:12)(cid:12)(cid:12) (cid:12)(cid:12)(cid:12)(cid:12) In other words, n > 2/ + 10 implies that as desired. rjh. Summer 2015: (10 points) suppose that {an} is a convergent sequence, say limn following: an = a. If an b for all n n, prove the (i) a b (ii) a sup n an.

Related Documents

MTH 320 Midterm: Math 320 Exam 2

turquoisegnu128

MTH 320 Midterm: Math 320 Exam 1

turquoisegnu128

MATH 355 Final: MATH 355 Amherst F14M355Final

turquoisegnu128

Related Questions

Need help with this study guide for my calculus 2 midterm. Please solve problems and show the solutions step by step for each problem. .

22

ey table is seen below xeecions tor Chapter 1 12, Fori, b â¬ Î.el * b-aa (0 (D 14 ForVEQ r the operation defined in Example 1 on the wr John Sue Henry. P iDFor 15ine if is ass ociative by determining if the final six engu defined ang property (ii)of Theorem 1 . So no element i if the operntion debined in Example 1 of Emle if each element has an inverse Section 1.3 Groups iw comutatityn ild Chapter 3 where the Funda the exercises that follow etermining why they are not Write out the Cayley table for the gru(o)nud lensify thee element the 10 elements of the group Z 18 its operation uses ts in the first coordinnte and +2 in the secotu Ldessity the Zn and write out the Cayley table. Reeall th of each element does Theorem 1.14 tell us aont the entries in the Cayley table ol s xrewp that is set with exactly one element. A {n), will always form group since there 19. What nly one way to define an operation on the set. Be sure to shhow that the properi combination of the usual notice what set the rule is be of a group all hold. 21. We can create even create groupe with games! Consider four cups placed in a ssare patter table. If we have a penny in one of the cups there are four ways we can move it to t cup: Horizontally, Vertically, Diagonally, or Stay nehere it is. We will p, S. To define nn operation, consider two movements in a row, v.e.,m ove the penny as r tells us to, then after that move the penny as y instruets. the set of integers the set of real numbers n the set of positive integers. e set of positive integers. n the set of positive integers. on the set of integers e set of negative integers. we ple, HV D since if we first move it horizontally and then vertically nltogether e moved it diagonally. Create the Cayley table for this group, identify the identity and the inverse of cach element 22. Prove that the set A 0 under matrix multiplication. Is it abelian? 23. Verify that 3(R) is a group using the addition of funetions as defined in Example 13 e set of nonzero rational n he set of nonzero real num n on the set R (-1 Section 1.4 Basic Algebra in Groups 24. Prove the Cancellation Law (Theorem 1.20). Do not use any theorems that occur after it in the text ssociative, commutative, has roof or counterexample fo 25. Assume G is a group and a e G. Consider a fixed integer k and use PMI (Theorem 0.3) to prove that for all nEN, a aYou will need to consider cases here since k can be positive, negative, or o 26. Prove Theorem 1.23 (ii) for the case of n > 0 and m

Please show 2-4