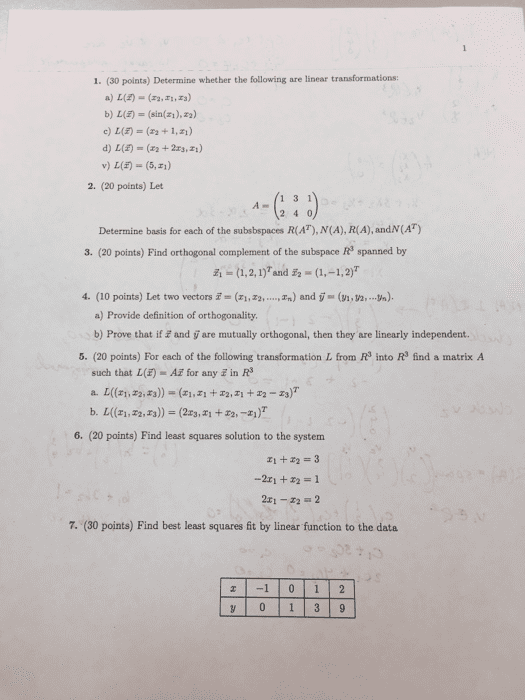M-221 Midterm: MATH 221 Montana State Exam3

• School: MSU
• Department: Mathematics
• Course: M-221
• Professor: All

Document Summary

Show proper work for full credit in problems 3-6: (2pts each) answer true or false. If a is an invertible matrix, then the column vectors of a must be linearly independent. (b) If a is an m n matrix, then row(a) is a subspace of rm. (c) If v is a subspace of r5 with dimension 3, then the orthogonal complement of v , v , must have dimension 2. (i. e. dim(v ) = 2) (d) Every subspace of dimension 1 in r2 is represented by a line that goes through the origin. (e) If a is an m n matrix with nullity(a) = 0, then col(a) = rm . (f) , ~vn} = rn, then the set {~v1, ~v2, . , ~vn} is linearly independent: (2pt each) short answer. Suppose a is a matrix with row(a) = span(cid:26)(cid:20) 3. Give the following: (i) the size of a is.