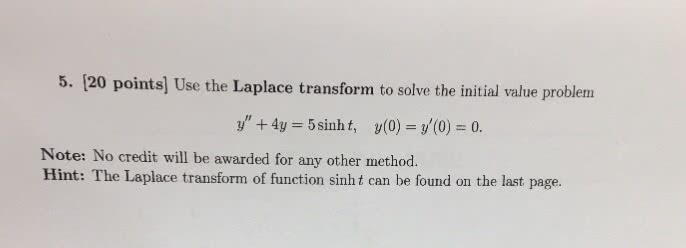MATH 0290 Midterm: Math 0290 Exam 2 (0290) 2016 Fall -188
Document Summary
Show all your work (no work = no credit). Simplify your answers when possible: (15 points) by using laplace transform solve the initial-value problem y + 4y = 4 cos 2t, y(0) = 0, y (0) = 0. Do not use the convolution: consider the initial-value problem y + y = g(t), y(0) = 0, where g(t) = . 0, t, for 0 t < 3 for t 3 (a) (5 points) describe the function g(t) in terms of the heaviside function. (b) (10 points) by using laplace transform solve the initial-value problem. 4 s + 1 (c) (5 points) create a piecewise de nition for your solution y(t) that does not contain the. Page 2: (20 points) use laplace transform and the convolution to nd a solution to the initial-value problem y + 4y = 2 t, y(0) = 1, y (0) = 6. Page 3: for the homogeneous linear system y .